 por Pessoa Estranha » Qui Jan 02, 2014 18:32
por Pessoa Estranha » Qui Jan 02, 2014 18:32
Olá, pessoal! Preciso de ajuda para concluir a seguinte questão:
"ESCREVA UMA EQUAÇÃO REDUZIDA DA ELIPSE DE EXCENTRICIDADE e = 3/5, SABENDO QUE DOIS VÉRTICES SÃO (5,0) E (-5,0) E QUE OS FOCOS ESTÃO EM Oy."
Na verdade a questão tem dois itens, mas o primeiro eu consegui resolver (ao invés de Oy era Ox).
Por favor, ajudem! Este segundo item não está fazendo sentido para mim.
Obrigada!
-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por young_jedi » Qui Jan 02, 2014 23:00
por young_jedi » Qui Jan 02, 2014 23:00
este segundo é similar ao primeiro caso que voce fez mais agora a equação tem o seguinte formato
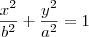
dos vertices temos que

da equação da excentricidade temos

teremos que
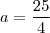
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por Pessoa Estranha » Qui Jan 02, 2014 23:32
por Pessoa Estranha » Qui Jan 02, 2014 23:32
Entendi!
Só a excentricidade que não costumo calcular assim. Mas, aplicando a maneira que uso em geral, temos:

Por outro lado,

.
Daí,
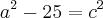
Assim,
![3a = 5(\sqrt[]{{a}^{2}-25}) \rightarrow 9{a}^{2} = 25{a}^{2} - 625 3a = 5(\sqrt[]{{a}^{2}-25}) \rightarrow 9{a}^{2} = 25{a}^{2} - 625](/latexrender/pictures/dbfb790844a161ca24ca65facc91aead.png)
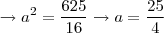
Você fez manipulação algébrica para chegar naquela fórmula para a excentricidade.... Entendi!
O que não estava fazendo sentido para mim eram os pontos dados.
Ok. Obrigada!


-
Pessoa Estranha
- Colaborador Voluntário

-
- Mensagens: 262
- Registrado em: Ter Jul 16, 2013 16:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Elipse
por Pessoa Estranha » Seg Dez 30, 2013 09:37
- 0 Respostas
- 1117 Exibições
- Última mensagem por Pessoa Estranha

Seg Dez 30, 2013 09:37
Geometria Analítica
-
- [Geometria Analítica] Elipse
por Pessoa Estranha » Qua Jan 01, 2014 01:27
- 3 Respostas
- 2743 Exibições
- Última mensagem por Renato_RJ

Qua Jan 01, 2014 15:15
Geometria Analítica
-
- [Geometria Analítica] Elipse
por Pessoa Estranha » Qui Jan 02, 2014 18:39
- 0 Respostas
- 1117 Exibições
- Última mensagem por Pessoa Estranha

Qui Jan 02, 2014 18:39
Geometria Analítica
-
- [Desafio] Geometria Analítica - Elipse
por Pessoa Estranha » Qui Jan 02, 2014 18:43
- 1 Respostas
- 5577 Exibições
- Última mensagem por teabiofeul

Seg Out 05, 2015 08:42
Desafios Enviados
-
- [Desafio] Geometria Analítica - Elipse
por Pessoa Estranha » Qui Jan 02, 2014 18:47
- 0 Respostas
- 4202 Exibições
- Última mensagem por Pessoa Estranha

Qui Jan 02, 2014 18:47
Desafios Enviados
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Exercicios de polinomios
Autor:
shaft - Qua Jun 30, 2010 17:30

Então, o exercicio pede para encontrar

.
Bom, tentei resolver a questão acima desenvolvendo as duas partes em ( )...Logo dps cheguei em um resultado q nao soube o q fazer mais.
Se vcs puderem ajudar !
Assunto:
Exercicios de polinomios
Autor:
Douglasm - Qua Jun 30, 2010 17:53
Bom, se desenvolvermos isso, encontramos:

Para que os polinômios sejam iguais, seus respectivos coeficientes devem ser iguais (ax = bx ; ax² = bx², etc.):


Somando a primeira e a segunda equação:

Finalmente:

Até a próxima.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


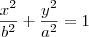


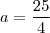

 .
.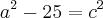
![3a = 5(\sqrt[]{{a}^{2}-25}) \rightarrow 9{a}^{2} = 25{a}^{2} - 625 3a = 5(\sqrt[]{{a}^{2}-25}) \rightarrow 9{a}^{2} = 25{a}^{2} - 625](/latexrender/pictures/dbfb790844a161ca24ca65facc91aead.png)
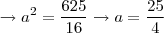



 .
.



