 por Fernando Macedo » Qua Nov 13, 2013 18:03
por Fernando Macedo » Qua Nov 13, 2013 18:03
qual a ideia e os conceitos de vetores e geometria analítica que devo ter quando me depara com questões como estas a seguir:
1) Dado uma triângulo qualquer ABC, seja M o ponto médio do lado AC e N o ponto médio do lado BC. Demonstre que MN é paralelo a AB e o vetor MN= 1/2AB(vetor)?
2) Mostre que as diagonais de uma paralelogramo cortam-se ao meio?
3) Demonstre que 0 segmento que une os pontos médios dos lados não paralelos de um trapézio é paralelo as bases e sua medida é a média aritmética das medidas das bases?
4) sejam os vetores a,b,c que representam as arestas de uma paralelepípedo. Expresse cada uma das quatro diagonais internas como combinação linear dos vetores a,b e c?
-
Fernando Macedo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 13, 2013 16:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em química
- Andamento: cursando
 por e8group » Qua Nov 13, 2013 20:01
por e8group » Qua Nov 13, 2013 20:01
Atenção , uma questão por tópico .
Vou ajudar com respeito ao exercício (2) . Considere O paralelogramo ABCD e suponhamos
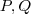
pontos médios das duas diagonais do paralelogramo . Vamos mostrar
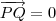
(aqui 0 representa vetor nulo ) ,o que é equivalente mostrar que
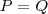
.
(Faça um desenho p/ auxiliar ) . Pela álgebra vetorial ,
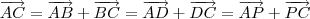
.

Agora tente mostrar através destas relações que
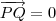
se não você não conseguir avançar comente .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
 por Fernando Macedo » Qua Nov 13, 2013 21:00
por Fernando Macedo » Qua Nov 13, 2013 21:00
UMA OBSERVAÇÃO QUE FIZ, VISUALIZANDO A IMAGEM DO PARALELOGRAMO, FOI QUE TODOS OS VETORES FORMAM UM TRIÂNGULO EM FUNÇÃO DE AC E DB, ENTÃO TENHO QUE FAZER O MESMO???
LOGO, PQ=PB+BQ=PC+CQ=PD+DQ.
MAS AI ME SURGIU UMA DUVIDA SE EU FORMA OS VETORES PA+AQ TAMBÉM FORMA UM TRIÂNGULO, SÓ QUE COM SENTIDO DIFERENTE?
-
Fernando Macedo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qua Nov 13, 2013 16:40
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em química
- Andamento: cursando
 por e8group » Qua Nov 13, 2013 22:14
por e8group » Qua Nov 13, 2013 22:14
Desculpe ,não conseguir compreender o que queres dizer . OBS.: No link abaixo encontra-se uma solução p/ este problema (veja ex.: 2)
http://fatosmatematicos.blogspot.com.br ... es-de.html . Espero que ajude .
-
e8group
- Colaborador Voluntário

-
- Mensagens: 1400
- Registrado em: Sex Jun 01, 2012 12:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Logaritmo] duas questões para resolução com urgência
por Cristian Cristiano » Qua Mai 03, 2017 04:37
- 0 Respostas
- 4055 Exibições
- Última mensagem por Cristian Cristiano

Qua Mai 03, 2017 04:37
Logaritmos
-
- resolução de questões
por emerson meneses » Ter Jul 07, 2009 17:28
- 0 Respostas
- 2253 Exibições
- Última mensagem por emerson meneses

Ter Jul 07, 2009 17:28
Geometria Analítica
-
- resolução de questões de matemática
por mauro arkader » Seg Abr 07, 2008 00:21
- 2 Respostas
- 38936 Exibições
- Última mensagem por lukas

Qua Jul 29, 2009 10:38
Álgebra Elementar
-
- [porcentagem] Ajuda para resolução
por Mimizinha » Qua Mar 19, 2008 14:39
- 2 Respostas
- 4792 Exibições
- Última mensagem por Mimizinha

Qua Mar 19, 2008 15:54
Álgebra Elementar
-
- Estrategias para resoluçao de limites
por Claudin » Dom Mai 15, 2011 14:13
- 7 Respostas
- 4026 Exibições
- Última mensagem por Claudin

Seg Mai 16, 2011 01:10
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


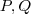 pontos médios das duas diagonais do paralelogramo . Vamos mostrar
pontos médios das duas diagonais do paralelogramo . Vamos mostrar 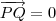 (aqui 0 representa vetor nulo ) ,o que é equivalente mostrar que
(aqui 0 representa vetor nulo ) ,o que é equivalente mostrar que 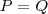 .
. 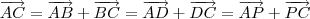


![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.