(Unifor-CE) A equação da circunferência que contém a origem, tem centro na reta x=2 e tangencia a reta x + y -4 = 0 é:
a) x² + y² + 4x - 4y + 4 = 0
b) x² + y² - 2x + 2y = 0
c) x² + y² - 4x + 4y = 0
d) x² + y² + 4x - 4y = 0
e) x² + y² - 4x + 4y + 4 = 0
A minha dificuldade nessa questão está em achar o y do centro, afinal para qualquer valor de y x valeria 2, assim y poderia assumir qualquer valor?


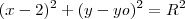
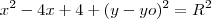 .
.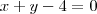 é tangente a circunferência. Note que o raio
é tangente a circunferência. Note que o raio 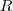 é a distância entre o centro e a própria reta. Portanto,
é a distância entre o centro e a própria reta. Portanto,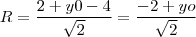
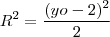
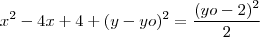
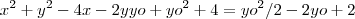
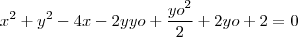
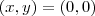 deve estar na circunferência então
deve estar na circunferência então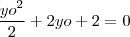
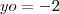 .
.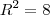 e
e 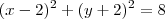
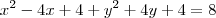
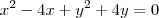


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)