Vamos fazer mudança de coordenadas .Para isto vamos associar ao eixo

e

,respectivamente ,a reta paralela(
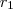
) e perpendicular(
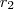
) à reta diretriz (dada) tais que ambas retas passam pela a mesma origem O.
Sejam
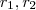
retas dadas por :
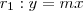
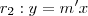
Podemos escrever a reta diretriz (dada) da seguinte forma :
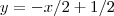
Sabemos que
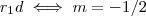
e
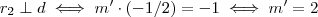
.
Assim ,

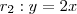
Para construirmos o novo sistema de coordenadas
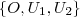
ortogonal precisaremos dos vetores
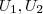
unitários e mutuamente ortogonais .
Tomando por exemplo

e substituindo-se

nas equações da reta
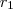
e
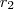
obtemos que os pontos
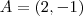
e
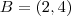
pertencem ,respectivamente ,à
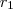
e
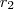
(Observe que
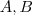
pontos são pontos dos eixos coordenados do novo sistema de coordenadas ortogonal) .
Através dos pontos obtidos acima podemos construir os vetores
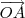
e
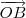
e tomar explcítamente
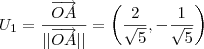
e
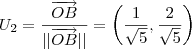
que são vetores mutuamente ortogonais e unitários .
Se
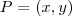
,devemos encontrar as coordenadas de P em relação ao novo sistema de coordenadas ,para isto ,devemos encontar
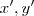
tais que
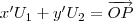
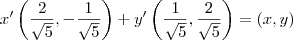
A equação acima é equivalente ao sistema linear
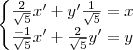
Ou ,
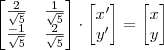
ou ainda
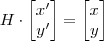
Em que
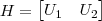
com U_1 ,U_2 matrizes colunas .
Multiplicando-se à esquerda por
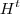
(deixo para você concluir que
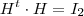
) ,obtemos :
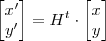
.
Desta forma ,as coordenadas de

em relação ao novo sistema são dadas por
![[P]_{\{O,U_1,U_2\}} = H^t \cdot \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{\sqrt{5}}\begin{bmatrix} 2 & -1 \\ 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{\sqrt{5}}\cdot\begin{bmatrix} 2x -y \\ x +2y\ \end{bmatrix} [P]_{\{O,U_1,U_2\}} = H^t \cdot \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{\sqrt{5}}\begin{bmatrix} 2 & -1 \\ 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{\sqrt{5}}\cdot\begin{bmatrix} 2x -y \\ x +2y\ \end{bmatrix}](/latexrender/pictures/2f48605f29bee6d68059e2d690d02b31.png)
.
Assim ,a equação diretriz em relação ao novo sistema é dada por :
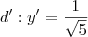
(por favor faças as contas) e o ponto
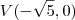
(vértice da parábola).
Agora seguiremos o seguinte o roteiro :
(1) Determinar o ponto
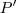
tal que
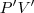
seja ortogonal a
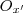
.
(2) Através do ponto
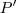
teremos o ponto
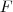
que é o foco da parábola (pois ,F é simétrico ao ponto P' em relação a V' )
(3) Uma vez que temos o foco F e equação da reta diretriz ,se
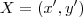
é o conjunto de pontos tais que

,então ao desenvolver esta expressão econtraremos a equação associada ao sistema
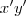
da parábola .(OBS.: as coordenadas de X é em relação ao novo sistema )
Segue então :
(1) É fácil ver que
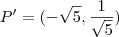
(Verifique !)
(2) Se o ponto F é simétrico de P' em relação a V' ,temos então que
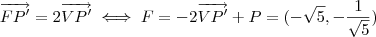
(3)
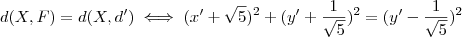
.
Simplificando :
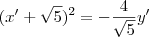
que é a equação da parábola em relação ao novo sistema . Para encontramos sua equação em relação ao sistema antigo ,substituiremos

por
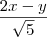
e

por
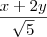
.
Assim ,temos :
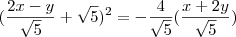
Simplificando :
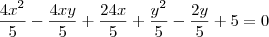
que é aquação da parábola em relação ao sistema antigo .
OBS .: Infelizmente o texto ficou muito grande ,por este motivo omitir algumas manipulações algébricas e contas ,mas se permanecer dúvidas mande de volta . Convenhamos é um pouco "trabalhoso " este processo de mudança de coordenadas ,mas até que é divertido .
Vou anexar uma imagem da parábola com suas propriedades .


 e
e  ,respectivamente ,a reta paralela(
,respectivamente ,a reta paralela( ) e perpendicular(
) e perpendicular( ) à reta diretriz (dada) tais que ambas retas passam pela a mesma origem O.
) à reta diretriz (dada) tais que ambas retas passam pela a mesma origem O.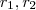 retas dadas por :
retas dadas por : 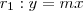
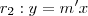
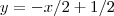
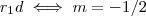 e
e 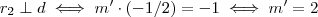 .
. 
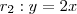
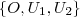 ortogonal precisaremos dos vetores
ortogonal precisaremos dos vetores 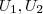 unitários e mutuamente ortogonais .
unitários e mutuamente ortogonais . e substituindo-se
e substituindo-se  nas equações da reta
nas equações da reta 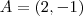 e
e 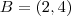 pertencem ,respectivamente ,à
pertencem ,respectivamente ,à 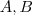 pontos são pontos dos eixos coordenados do novo sistema de coordenadas ortogonal) .
pontos são pontos dos eixos coordenados do novo sistema de coordenadas ortogonal) . 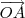 e
e 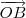 e tomar explcítamente
e tomar explcítamente 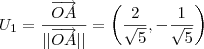 e
e 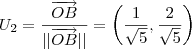 que são vetores mutuamente ortogonais e unitários .
que são vetores mutuamente ortogonais e unitários . 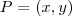 ,devemos encontrar as coordenadas de P em relação ao novo sistema de coordenadas ,para isto ,devemos encontar
,devemos encontrar as coordenadas de P em relação ao novo sistema de coordenadas ,para isto ,devemos encontar 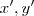 tais que
tais que 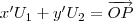
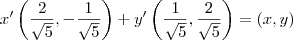
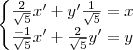
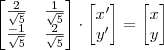
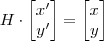
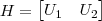 com U_1 ,U_2 matrizes colunas .
com U_1 ,U_2 matrizes colunas .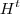 (deixo para você concluir que
(deixo para você concluir que 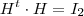 ) ,obtemos :
) ,obtemos : 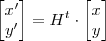 .
. em relação ao novo sistema são dadas por
em relação ao novo sistema são dadas por ![[P]_{\{O,U_1,U_2\}} = H^t \cdot \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{\sqrt{5}}\begin{bmatrix} 2 & -1 \\ 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{\sqrt{5}}\cdot\begin{bmatrix} 2x -y \\ x +2y\ \end{bmatrix} [P]_{\{O,U_1,U_2\}} = H^t \cdot \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{\sqrt{5}}\begin{bmatrix} 2 & -1 \\ 1 & 2 \end{bmatrix} \cdot \begin{bmatrix} x\\y \end{bmatrix} = \frac{1}{\sqrt{5}}\cdot\begin{bmatrix} 2x -y \\ x +2y\ \end{bmatrix}](/latexrender/pictures/2f48605f29bee6d68059e2d690d02b31.png) .
.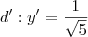 (por favor faças as contas) e o ponto
(por favor faças as contas) e o ponto 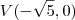 (vértice da parábola).
(vértice da parábola).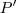 tal que
tal que 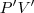 seja ortogonal a
seja ortogonal a 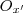 .
. 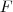 que é o foco da parábola (pois ,F é simétrico ao ponto P' em relação a V' )
que é o foco da parábola (pois ,F é simétrico ao ponto P' em relação a V' ) 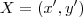 é o conjunto de pontos tais que
é o conjunto de pontos tais que  ,então ao desenvolver esta expressão econtraremos a equação associada ao sistema
,então ao desenvolver esta expressão econtraremos a equação associada ao sistema 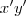 da parábola .(OBS.: as coordenadas de X é em relação ao novo sistema )
da parábola .(OBS.: as coordenadas de X é em relação ao novo sistema )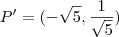 (Verifique !)
(Verifique !)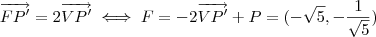
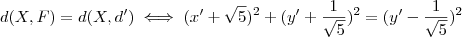 .
.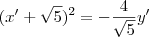 que é a equação da parábola em relação ao novo sistema . Para encontramos sua equação em relação ao sistema antigo ,substituiremos
que é a equação da parábola em relação ao novo sistema . Para encontramos sua equação em relação ao sistema antigo ,substituiremos 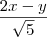 e
e 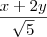 .
. 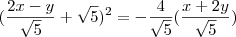
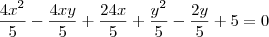 que é aquação da parábola em relação ao sistema antigo .
que é aquação da parábola em relação ao sistema antigo . 

 e do
e do  ,todos estão associados ao novo sistema de coordenadas .Segue
,todos estão associados ao novo sistema de coordenadas .Segue 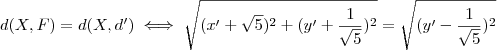 .
.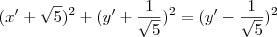 .
.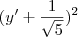 e
e 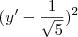 observaremos que os termos
observaremos que os termos 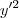 e
e 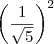 ] que são comuns a ambas expressões se cancelaram (basta addcionar o simétrico[ou oposto] deles em ambos membros ) ,desta forma ficaremos com
] que são comuns a ambas expressões se cancelaram (basta addcionar o simétrico[ou oposto] deles em ambos membros ) ,desta forma ficaremos com 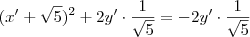 .
. 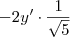 em ambos membros , segue
em ambos membros , segue 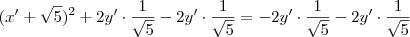
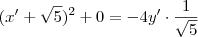
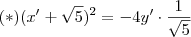 que é a equação da parábola em relação ao novo sistema de coordenadas ,significa que se
que é a equação da parábola em relação ao novo sistema de coordenadas ,significa que se 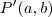 é um ponto da parábola, então
é um ponto da parábola, então  é solução da equação
é solução da equação ,caso contrário não o é .
,caso contrário não o é . ![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.