 por manuoliveira » Ter Nov 27, 2012 15:19
por manuoliveira » Ter Nov 27, 2012 15:19
Determine o plano que seja paralelo ao plano z = 2x + 3y e tangente ao gráfico de f(x, y) = x² + xy
Tenho prova amanhã! Me ajudemmm!!
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
 por young_jedi » Ter Nov 27, 2012 16:53
por young_jedi » Ter Nov 27, 2012 16:53
primeiro encontrar o vetor normal do plano
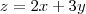

portanto o vetor normal sera (2,3,-1)
agora calculando

nos temos o vetor
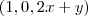
e calculando
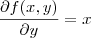
nos temos o vetor
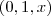
ambos os vetores são perpendiculares ao vetor normal ao plano portanto

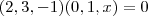
então
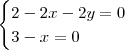
então x=3 e y=-2
portanto

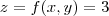
portanto o plano sera
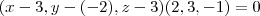


-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por manuoliveira » Ter Nov 27, 2012 22:40
por manuoliveira » Ter Nov 27, 2012 22:40
Obrigada!!
-
manuoliveira
- Usuário Parceiro

-
- Mensagens: 61
- Registrado em: Qui Abr 01, 2010 19:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Química
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Retas e Planos - Resolução de Exercícios URGENTE
por Dyego Dias » Seg Nov 18, 2013 20:21
- 0 Respostas
- 1755 Exibições
- Última mensagem por Dyego Dias

Seg Nov 18, 2013 20:21
Geometria Analítica
-
- [Estudo das Retas e Planos] URGENTE! Duvida Exercicio
por fernandobosso » Sáb Mai 04, 2013 21:35
- 0 Respostas
- 1135 Exibições
- Última mensagem por fernandobosso

Sáb Mai 04, 2013 21:35
Geometria Analítica
-
- PLANOS - PARALELISMO ENTRE PLANOS
por ubelima » Ter Jun 19, 2012 19:22
- 2 Respostas
- 5828 Exibições
- Última mensagem por ubelima

Qua Jun 20, 2012 01:01
Geometria Analítica
-
- Planos
por nayarabarbosa » Ter Set 17, 2013 10:44
- 0 Respostas
- 1101 Exibições
- Última mensagem por nayarabarbosa

Ter Set 17, 2013 10:44
Geometria Analítica
-
- planos projetivos
por Ritinhasj » Seg Set 14, 2009 13:01
- 1 Respostas
- 1593 Exibições
- Última mensagem por Ritinhasj

Qua Set 16, 2009 12:30
Geometria Plana
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



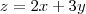


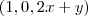
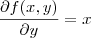
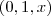

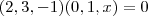
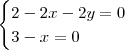

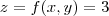
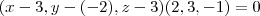




 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.