 por renan_a » Seg Out 01, 2012 19:32
por renan_a » Seg Out 01, 2012 19:32
Obtenha uma equação vetorial para a reta l que passa por P(2,-1,1) e é concorrente com as retas reversas.
r: y+z=5 , x-2z=9
s: 2x-z+1=0 , y - 2z = 1
--------------
Sei que já tenho o ponto P, preciso descobrir o ponto Q para fazer o vetor PQ e formar a equação geral.
Engraçado é que aprendi por aqui mesmo, um exercício semelhante, só que eu tinha um vetor u já, e tinha que obter os pontos M e N.
Nesse tá mais complicado.
Agradeço desde agora a ajuda dos amigos. Abraços
-
renan_a
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Ter Set 25, 2012 08:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por young_jedi » Seg Out 01, 2012 19:55
por young_jedi » Seg Out 01, 2012 19:55
sendo Q um ponto pertencente a r e a l e A um ponto pertencente a s e a l temos que
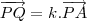
onde k é um valor real qualquer com isso acho que da pra chegar a resposta
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
 por renan_a » Seg Out 01, 2012 20:14
por renan_a » Seg Out 01, 2012 20:14
se eu chamar z=t na reta r e z=h na reta s, descubro um dos pontos pertencentes às duas retas.
r: z=t , x=9+2t , y5-2t
s: z=h, x= -1/2 + h/2, y=1 + 2h
São esses pontos que devo usar para descobrir o PQ e PA??
-
renan_a
- Usuário Dedicado

-
- Mensagens: 32
- Registrado em: Ter Set 25, 2012 08:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Mecânica
- Andamento: cursando
 por young_jedi » Seg Out 01, 2012 22:04
por young_jedi » Seg Out 01, 2012 22:04
isso mesmo com esses dois pontos voce equaciona o exercicio
-
young_jedi
- Colaborador Voluntário

-
- Mensagens: 1239
- Registrado em: Dom Set 09, 2012 10:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Elétrica - UEL
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [RETAS] equação vetorial
 por renan_a » Qua Set 26, 2012 19:59
por renan_a » Qua Set 26, 2012 19:59
- 10 Respostas
- 8099 Exibições
- Última mensagem por renan_a

Seg Out 01, 2012 20:16
Geometria Analítica
-
- Equação geral do plano usando duas retas
por iarapassos » Sáb Set 01, 2012 19:12
- 2 Respostas
- 8782 Exibições
- Última mensagem por iarapassos

Dom Set 02, 2012 22:15
Geometria Analítica
-
- [Equação de reta] - duas dúvidas
por MrJuniorFerr » Sex Out 12, 2012 22:03
- 3 Respostas
- 1774 Exibições
- Última mensagem por young_jedi

Sáb Out 13, 2012 11:14
Geometria Analítica
-
- Equação vetorial da reta
por Danilo » Qua Out 31, 2012 02:36
- 3 Respostas
- 2325 Exibições
- Última mensagem por MarceloFantini

Sex Nov 02, 2012 08:23
Geometria Analítica
-
- Equação vetorial da reta/plano
por Danilo » Dom Nov 04, 2012 13:23
- 2 Respostas
- 4884 Exibições
- Última mensagem por Danilo

Dom Nov 04, 2012 16:51
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Balanar - Seg Ago 09, 2010 04:01
Simplifique a expressão com radicais duplos abaixo:
![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
Resposta:
Dica:
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
(dica : igualar a expressão a

e elevar ao quadrado os dois lados)
Assunto:
Simplifique a expressão com radicais duplos
Autor:
MarceloFantini - Qua Ago 11, 2010 05:46
É só fazer a dica.
Assunto:
Simplifique a expressão com radicais duplos
Autor:
Soprano - Sex Mar 04, 2016 09:49
Olá,
O resultado é igual a 1, certo?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


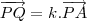

![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)