 por IsadoraOliveira » Sex Set 28, 2012 16:23
por IsadoraOliveira » Sex Set 28, 2012 16:23
Sejam u(u1,u2,u3) e v(v1,v2,v3) e
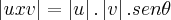
, onde

é o ângulo entre os vetores u e v, mostre que
u x v =
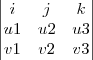
OBS:
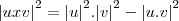
OBS2: Leve em consideração as propriedades de produto vetorial
Eu recebi esse desafio na faculdade, mas não to sabendo por onde começar e nem to tendo muita noção do que fazer. Tem como alguém me ajudar?
Vlww
-
IsadoraOliveira
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Sex Set 28, 2012 15:43
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Sex Set 28, 2012 17:51
por Russman » Sex Set 28, 2012 17:51
O produto vetorial de vetores se assemelha ao produto de escalares. Dado um escalar real
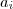
então, por exemplo
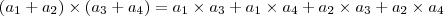
,
isto é, o produto de somas é chamado
distributivo.
Assim, dados dois vetores
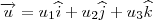
e
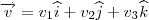
, temos
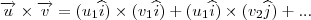
.
Faça para todos os termos. Lembre-se que
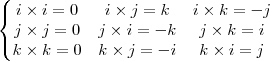
e que
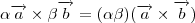
, alpha e beta escalares.
Rearranjando os termos você identificará a mesma configuração de um determinante de matriz 3x3 dada organização como é exposto o produto vetorial.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Produto Vetorial] Exercício de vetores
por bobkaladao » Dom Nov 06, 2011 20:18
- 1 Respostas
- 2599 Exibições
- Última mensagem por LuizAquino

Dom Nov 06, 2011 23:17
Geometria Analítica
-
- [Produto entre vetores] Escalar e vetorial
por ViniciusAlmeida » Qui Abr 23, 2015 23:36
- 1 Respostas
- 3112 Exibições
- Última mensagem por DanielFerreira

Sex Abr 24, 2015 21:24
Geometria Analítica
-
- Produto Vetorial - Medida angular entre os vetores
por talesalberto » Seg Nov 03, 2014 21:42
- 1 Respostas
- 2252 Exibições
- Última mensagem por Russman

Ter Nov 04, 2014 01:31
Geometria Analítica
-
- Produto escalar, Produto Vetorial e Produto Misto
 por fernando7 » Qua Mai 23, 2018 17:29
por fernando7 » Qua Mai 23, 2018 17:29
- 0 Respostas
- 4946 Exibições
- Última mensagem por fernando7

Qua Mai 23, 2018 17:29
Geometria Analítica
-
- [Vetores] Produto Entre Vetores
por _bruno94 » Qua Jul 10, 2013 00:34
- 1 Respostas
- 5210 Exibições
- Última mensagem por temujin

Qua Jul 10, 2013 14:27
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
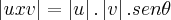 , onde
, onde  é o ângulo entre os vetores u e v, mostre que
é o ângulo entre os vetores u e v, mostre que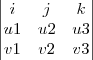
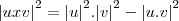


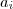 então, por exemplo
então, por exemplo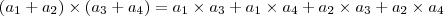 ,
,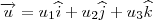 e
e 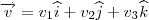 , temos
, temos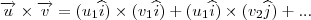 .
.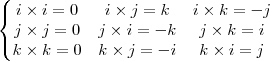
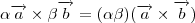 , alpha e beta escalares.
, alpha e beta escalares.
