 por iarapassos » Sáb Set 01, 2012 22:07
por iarapassos » Sáb Set 01, 2012 22:07
Considere a reta s o ponto Q e o plano a seguir:
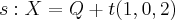
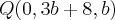
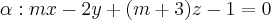
Determine b e m, de modo que a reta s seja paralela ao plano alpha.
Se a reta s é paralela a alpha, logo:
o vetor diretor de s é ortogonal ao vetor normal de alpha.
v.n=0.
Temos que v=(1,0,2) e n=(m,-2,m+3)
Como (1,0,2).(m,-2,m+3)=0
calculando, temos m=-2.
Massa! E como faço agora para achar b?
-
iarapassos
- Usuário Ativo

-
- Mensagens: 23
- Registrado em: Qua Ago 29, 2012 12:34
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Controle e Automação
- Andamento: cursando
 por LuizAquino » Sáb Set 01, 2012 23:57
por LuizAquino » Sáb Set 01, 2012 23:57
iarapassos escreveu:Considere a reta s o ponto Q e o plano a seguir:
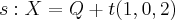
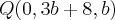
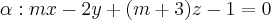
Determine b e m, de modo que a reta s seja paralela ao plano alpha.
Se a reta s é paralela a alpha, logo:
o vetor diretor de s é ortogonal ao vetor normal de alpha.
v.n=0.
Temos que v=(1,0,2) e n=(m,-2,m+3)
Como (1,0,2).(m,-2,m+3)=0
calculando, temos m=-2.
Massa! E como faço agora para achar b?
Bem, quando uma reta é paralela a um plano temos dois casos: a reta não está contida no plano; a reta está contida no plano;
Alguns autores excluem o caso da reta está contida no plano como sendo um caso particular de reta paralela a um plano.
Se esse for o caso do material onde você tirou esse exercício, então nenhum ponto da reta r pode estar no plano

. Desse modo, o ponto Q não pode pertencer ao plano. Tente continuar a partir daí.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Equações de plano] encontrar a equação de um plano
por GHT1810 » Ter Jul 03, 2018 19:42
- 0 Respostas
- 5361 Exibições
- Última mensagem por GHT1810

Ter Jul 03, 2018 19:42
Geometria Analítica
-
- [´PLANO] Ponto de intersecção de reta com plano
por manuel_pato1 » Ter Set 25, 2012 09:48
- 1 Respostas
- 14956 Exibições
- Última mensagem por LuizAquino

Ter Set 25, 2012 12:11
Geometria Analítica
-
- [Equação do Plano Tangente - Plano Paralalelo]
por raimundoocjr » Qui Out 24, 2013 22:10
- 0 Respostas
- 2941 Exibições
- Última mensagem por raimundoocjr

Qui Out 24, 2013 22:10
Cálculo: Limites, Derivadas e Integrais
-
- Plano
por Rhyu » Dom Abr 08, 2012 10:57
- 2 Respostas
- 1986 Exibições
- Última mensagem por MarceloFantini

Seg Abr 09, 2012 03:40
Geometria Analítica
-
- Plano
por Claudin » Sex Jul 06, 2012 12:32
- 2 Respostas
- 1810 Exibições
- Última mensagem por Claudin

Sex Jul 06, 2012 16:23
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
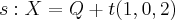
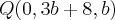
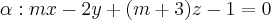


 . Desse modo, o ponto Q não pode pertencer ao plano. Tente continuar a partir daí.
. Desse modo, o ponto Q não pode pertencer ao plano. Tente continuar a partir daí.