Par de segmentos

[Cleyson007]

Bom dia a todos!

Verifique se o par de segmento AB e CD está em reta paralela ou coincidente. Em caso afirmativo, mostre geometricamente, se possui o mesmo sentido ou sentido oposto.

A = (0,?2), B = (2, 2), C = (0, 1), D = (?1,?1).

Estou resolvendo assim:

e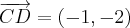

Coeficiente angular entre os vetores

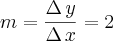
Como prosseguir?

No aguardo.

[e8group]

Olá boa tarde .Eu tentaria assim ,veja :


Solução 1 .


Sejam as retas onde os pontos , e 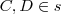e os vetores e são diretores as retas .Assim temos que ,





.


(continue)...



Solução 2 .


A equação da reta é da forma y = ax +b . Use o dados do enunciado e expresse as equações das retas .

[Cleyson007]

Boa noite Santhiago!

Vou trabalhar com a solução 2, parece-me mais fácil:

A = (0,1) e B = (-1,-1)

y = ax + b --> -2 = 0a + b e 2 = 2a + b --> y = 2x - 2 (Equação da reta AB)

C = (0,-2) e D = (2,2)

y = ax + b --> 1 = 0a + b e -1 = -a + b --> y = 2x + 1 (Equação da reta CD)

Como as retas possuem o mesmo coeficiente angular (m = 2), logo são paralelas.

Santhiago, gostaria de saber, se somente pelo fato de possuirem o mesmo coeficiente angular posso afirmar que são paralelas.

Aguardo retorno.

[e8group]

Boa noite ,

Santhiago, gostaria de saber, se somente pelo fato de possuirem o mesmo coeficiente angular posso afirmar que são paralelas.

Aguardo retorno.

Sim .


Na minha opinião ,uma outra forma de verificar se a as retas são paralelas é analisar se as componentes dos vetores diretores são proporcionais entre-si ,isto é :

(utilizando o enunciado como exemplo)

.

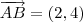Perceba que pelos pontos dado no enunciado ,temos e 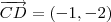.Como podemos ver é uma forma verificar se as retas são paralelas ,certo ?

[Cleyson007]

Boa tarde,

correto Santhiago!

Obrigado pela atenção.

Cleyson007