A questão é a seguinte: Sabendo-se que os pontos P e Q pertencem a reta x=3 e estão a uma distância d =3
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) u.c. da reta y= x +1, pode-se concluir que o segmento PQ mede, em u.c.:
u.c. da reta y= x +1, pode-se concluir que o segmento PQ mede, em u.c.:a) 15
b) 12
c) 9
d)6
e)5
Eu tentei fazer pela fórmula de distancia de ponto a reta, e achei -XP+YP-1 =0 . Depois disso, empaquei. Não faço a mínima ideia pra onde isso vai... ele não me deu as coordenadas de nada. Sem falar que não entrou na minha cabeça como a distancia entre dois pontos de uma reta constante e um ponto de uma reta inclinada podem ser iguais... é isso. Sou péssima em analítica, tenho várias dúvidas nesse assunto e não queria perder uma questão assim se aparecer na prova. Se alguma boa alma puder me explicar, agradecerei eternamente



 , então
, então  e
e  . Esta reta se encontra com a reta
. Esta reta se encontra com a reta  no ponto
no ponto 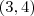 . Podemos assumir que P está acima da reta
. Podemos assumir que P está acima da reta  e
e  .
.  . Vamos escolher um dos pontos, por exemplo Q, e trabalhar com isso.
. Vamos escolher um dos pontos, por exemplo Q, e trabalhar com isso. .
.
 .
. .
.
 .
. e
e  . O segmento PQ é apenas a distância entre as ordenadas, daí
. O segmento PQ é apenas a distância entre as ordenadas, daí 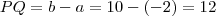 .
.


 .
.
 :
: