 por watson » Sáb Jun 02, 2012 16:42
por watson » Sáb Jun 02, 2012 16:42
Pessoal Boa tarde !
Aguem pode me ajudar .
Dados os vetores u=(2 -1 3) e v= (-2 1 2 ) determine o angulo entre vetores .
E a outra é determine um vetor u tal que u.v = u.w=1 e IuI= raiz 22 onde v=(1 1 0) e w (2 1 -1 )
Muito Obrigado
-
watson
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Fev 22, 2012 16:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Sáb Jun 02, 2012 17:49
por Russman » Sáb Jun 02, 2012 17:49
A solução de ambos é puramente a aplicação de teoria, são fundamentais!
O angulo

entre dois vetores

e
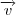
é dado por:

Tente aplicar este resultado.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por watson » Dom Jun 03, 2012 12:44
por watson » Dom Jun 03, 2012 12:44
Bom dia !
Desculpe me mas como faço essa conta ?
Obrigado
Watson
-
watson
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Fev 22, 2012 16:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por Russman » Dom Jun 03, 2012 18:34
por Russman » Dom Jun 03, 2012 18:34
watson escreveu:u=(2 -1 3) e v= (-2 1 2 )
u.v = 2.(-2) + (-1).1+3.2=-4-1+6= 1
mod v = (2²+1²+2²)^(1/2) = 3
mod u = (2²+1²+3²)^(1/2) = 14^1/2
theta = arcos( 1/(3.14^1/2))=~ 84°
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por watson » Dom Jun 03, 2012 19:18
por watson » Dom Jun 03, 2012 19:18
Muito Obrigado Agora entendi !!!
-
watson
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Qua Fev 22, 2012 16:20
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ângulo entre vetores
por ARCS » Qui Jun 02, 2011 09:20
- 4 Respostas
- 2686 Exibições
- Última mensagem por guermandi

Qui Jun 02, 2011 16:10
Geometria Analítica
-
- Angulo entre vetores
por Anne2011 » Sáb Jun 25, 2011 04:17
- 5 Respostas
- 4894 Exibições
- Última mensagem por LuizAquino

Dom Jun 26, 2011 10:44
Geometria Analítica
-
- Angulo entre vetores
 por matematicaead » Qui Out 27, 2011 17:45
por matematicaead » Qui Out 27, 2011 17:45
- 1 Respostas
- 5355 Exibições
- Última mensagem por LuizAquino

Qui Out 27, 2011 23:06
Geometria Analítica
-
- ângulo entre os vetores
por Ana Maria da Silva » Seg Abr 08, 2013 19:09
- 0 Respostas
- 902 Exibições
- Última mensagem por Ana Maria da Silva

Seg Abr 08, 2013 19:09
Geometria Analítica
-
- Angulo entre retas {vetores}
por Danilo » Ter Nov 06, 2012 16:07
- 3 Respostas
- 3053 Exibições
- Última mensagem por young_jedi

Qui Nov 08, 2012 10:20
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



 entre dois vetores
entre dois vetores  e
e 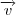 é dado por:
é dado por:




