wanderley argenton escreveu:Determinar o ponto B da reta s,de tal forma que o segmento AB intercepte a reta r no ponto C,que o divide na razão de 1/2.São dados:A(-3,1),
(r)x+y=0 e (s)2y-3x+1=0.
wanderley argenton escreveu:Em tempo:Cheguei a determinar o ponto de intersecção das duas retas r e s. Montei o gráfico,com os dados disponíveis e só.
Como B está sobre a reta s : 2y - 3x + 1 = 0, então esse ponto possui o formato
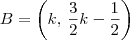
, para algum número k.
Como A = (-3, 1) e C é o ponto médio entre A e B (já que C divide o segmento AB na razão de 1/2), temos que
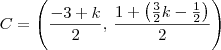
. Ou seja, temos que

.
Por outro lado, como C é um ponto da reta r : x + y = 0, temos que as suas coordenadas devem atender essa equação. Isto é, devemos ter:

Agora tente concluir o exercício.


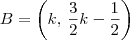 , para algum número k.
, para algum número k.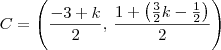 . Ou seja, temos que
. Ou seja, temos que  .
.

 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.