Excentricidade elipse

[CarolMarques]

Dê as condições sobre a excentricidade da elipse de equação x²/a² + y²/b²=1 para que seus focos pertençam à coroa fundamental.

Não sei o que fazer. A única coisa que eu fiz foi o desenho da coroa e o raio da menor é igual a b.

[LuizAquino]

Dê as condições sobre a excentricidade da elipse de equação x²/a² + y²/b²=1 para que seus focos pertençam à coroa fundamental.

Não sei o que fazer. A única coisa que eu fiz foi o desenho da coroa e o raio da menor é igual a b.

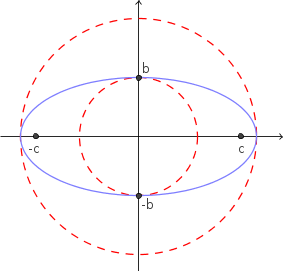
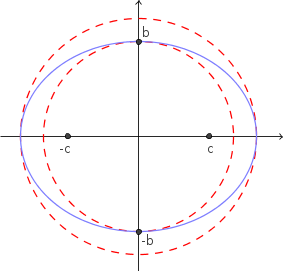
Observe as figuras abaixo.

figura1.png (8.2 KiB) Exibido 873 vezes

figura2.png (9.29 KiB) Exibido 873 vezes

figura3.png (9.81 KiB) Exibido 873 vezes

Note que quando os focos (-c, 0) e (c, 0) estão dentro da coroa circular, temos que c > b.

Já quando os focos estão sobre a circunferência menor, temos que c = b.

Por fim, quando os focos estão fora da coroa circular, temos que c < b.

Agora tente analisar o que essas informações implicam na excentricidade da elipse.