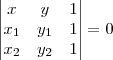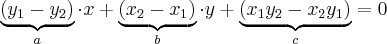Olá Christianobelli, seja bem-vindo!
Ainda é necessário dizer que este determinante deve ser nulo para encontrarmos a equação geral da reta:
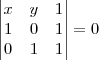
Então, além da importância da sua pergunta, também valeria o comentário sobre o "zero".
Há um conjunto de argumentos que justificam esta coluna com 1.
Vamos caminhar por eles e após este percurso, sua pergunta estará respondida.
O primeiro passo é retornar um pouco no conceito da
condição para alinhamento de três pontos.
De fato, sua pergunta surge nesta condição, pois a obtenção da equação da reta é nada mais do que a utilização deste teorema:
Três pontos

,
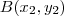
e
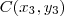
, são colineares se, e somente se:
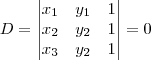
Perceba que na obtenção da equação geral da reta, B e C são pontos distintos do plano cartesiano, de modo que
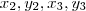
são números reais (constantes) conhecidos. E se o ponto
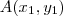
percorre a reta, então

e

são variáveis.
Esta condição de colinearidade entre os três pontos, é que nos permite obter a equação geral da reta daquela forma.
Então, agora podemos discutir sobre a coluna completada com 1, refletindo sobre a condição para alinhamento de três pontos.
Para isso, vamos procurar "descobrir" quais deveriam ser os números

,

e

:
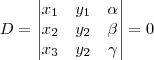
Devemos nos perguntar: quais as formas possíveis do alinhamento entre três pontos distintos, em relação aos eixos?
Há três possibilidades, em uma delas os A, B e C possuem a mesma ordenada, ou seja, estão alinhados horizontalmente, de modo que:
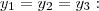
Lembrando de outra propriedade que também pode ser demonstrada é que se uma matriz M, de ordem

, tem duas filas paralelas (duas linhas ou duas colunas) formadas por elementos respectivamente
proporcionais, então det M = 0.
Neste caso atual que estamos analisando, procuramos

,

e

que sejam respectivamente proporcionais a

,

e
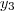
, mas

, com
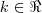
, o que implica em

como a única possibilidade que atende à proporcionalidade.
A nulidade do determinante é conseqüência da proporcionalidade entre a 2ª e 3ª colunas.
Em outra possibilidade, A, B e C possuem a mesma abscissa, ou seja, estão alinhados verticalmente, de modo que:
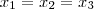
:
Analogamente, neste caso, procuramos

,

e

que sejam respectivamente proporcionais a

,

e
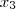
, mas
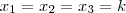
, com
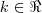
, também implicando em

como a única possibilidade que atende à proporcionalidade.
Aqui, a nulidade do determinante é conseqüência da proporcionalidade entre a 1ª e 3ª colunas.
A terceira possibilidade para o alinhamento dos pontos ocorre quando a reta que os contém, não é paralela nem ao eixo x, nem ao eixo y:
Pela semelhança dos triângulos ABD e BCE, temos a seguinte proporção:
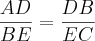
E utilizando as coordenadas:
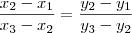

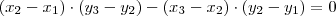
Fazendo a distributiva:
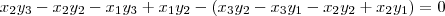
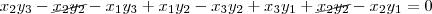
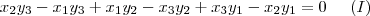
E comparando com o determinante, para obtermos

,

e

:
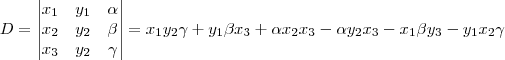
Para que

e reordenando as parcelas:
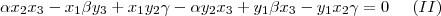
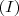
e
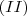


.
Vale ressaltar que consideramos pontos A, B e C distintos.
Caso dois dos pontos sejam coincidentes, a matriz terá um par de linhas iguais, e, analogamente, a nulidade do determinante resultará que

, da mesma forma.
Também cabe uma demonstração para a recíproca (volta
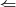
) do teorema que é verdadeira, ou seja, se

, A, B e C são colineares.
Veja que além de termos provado o teorema (ida

) de que três pontos

,
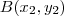
e
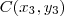
, são colineares se, e somente se:
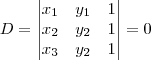
Fizemos o questionamento sobre

,

e

, supondo desconhecer que a 3º coluna possui os termos iguas a 1:
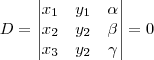
E verificamos que para que as condições da colinearidade sejam atendidas, em todos os casos possíveis, necessariamente,

.
Por fim, retornando ao caso da obtenção da equação geral da reta, conforme comentado, o que ocorre é uma utilização direta deste teorema, considerando que os dois pontos conhecidos
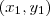
e
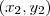
pentencem à reta.
Consideramos um ponto genérico
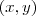
que percorre toda a reta e estabelecemos a condição de colinearidade do teorema aos outros dois conhecidos, ficando:
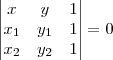
O desenvolvimento deste determinante resultará na equação geral da reta:
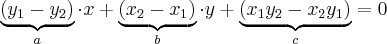
Christianobelli, devo comentar que muitas vezes as perguntas mais simples não possuem respostas tão diretas.
De qualquer forma, espero ter ajudado!


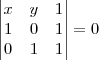
 ,
, 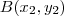 e
e 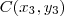 , são colineares se, e somente se:
, são colineares se, e somente se: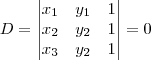
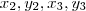 são números reais (constantes) conhecidos. E se o ponto
são números reais (constantes) conhecidos. E se o ponto 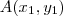 percorre a reta, então
percorre a reta, então  e
e  são variáveis.
são variáveis. ,
,  e
e  :
: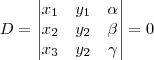
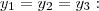
 , tem duas filas paralelas (duas linhas ou duas colunas) formadas por elementos respectivamente
, tem duas filas paralelas (duas linhas ou duas colunas) formadas por elementos respectivamente  e
e 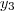 , mas
, mas  , com
, com 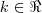 , o que implica em
, o que implica em  como a única possibilidade que atende à proporcionalidade.
como a única possibilidade que atende à proporcionalidade.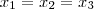 :
: e
e 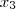 , mas
, mas 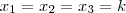 , com
, com 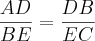
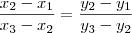

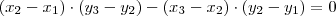
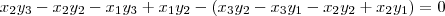
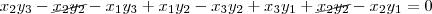
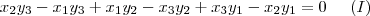
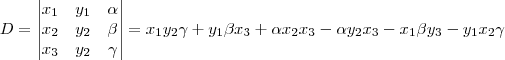
 e reordenando as parcelas:
e reordenando as parcelas: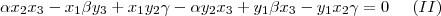
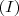 e
e 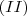

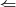 ) do teorema que é verdadeira, ou seja, se
) do teorema que é verdadeira, ou seja, se  , A, B e C são colineares.
, A, B e C são colineares.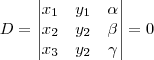
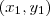 e
e 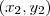 pentencem à reta.
pentencem à reta.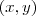 que percorre toda a reta e estabelecemos a condição de colinearidade do teorema aos outros dois conhecidos, ficando:
que percorre toda a reta e estabelecemos a condição de colinearidade do teorema aos outros dois conhecidos, ficando: