 por Dayannearaujo » Qui Abr 19, 2012 17:21
por Dayannearaujo » Qui Abr 19, 2012 17:21
a questão é a seguinte: Dois vértices de um triangulo são A(4,1) e B(10,4). Determine as coordenadas do terceiro ponto sabendo que a area é 36,6 e que o trinagulo é retangulo.
eu consegui fazer uma parte do exercicio:
AB * AC
(10-4)i + (4-1)j * (x-4)i + (y-1)j
6i*(x-4)i + 3j*(y-1)j
6x+3y-27 = 0 ---> primeira equação
resolve-se a matriz:
i j k
6 3 0
x-4 y-1 0, obtendo-se: k*(6y-6) - (3x - 12)
agora eu não consegui sair dai, sei que tem q elevar ao quadrado, mas nao sei por onde começar! me ajudeeem! esse trabalho é pra amanha, vale bem nota! :/
obrigada.
-
Dayannearaujo
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Qui Abr 19, 2012 17:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: engenharia civil
- Andamento: cursando
 por LuizAquino » Sex Abr 20, 2012 00:07
por LuizAquino » Sex Abr 20, 2012 00:07
Dayannearaujo escreveu:a questão é a seguinte: Dois vértices de um triangulo são A(4,1) e B(10,4). Determine as coordenadas do terceiro ponto sabendo que a area é 36,6 e que o trinagulo é retangulo.
Dayannearaujo escreveu:eu consegui fazer uma parte do exercicio:
AB * AC
(10-4)i + (4-1)j * (x-4)i + (y-1)j
6i*(x-4)i + 3j*(y-1)j
6x+3y-27 = 0 ---> primeira equação
Nesse caso, você está considerando que o ângulo reto está no vértice A. Como o exercício não especificou em qual vértice esse ângulo está, então na verdade a resolução deveria ser dividida em três casos: ângulo reto em A; ângulo reto em B; ângulo reto em C.
Dayannearaujo escreveu:resolve-se a matriz:
i j k
6 3 0
x-4 y-1 0, obtendo-se: k*(6y-6) - (3x - 12)
Você sabe que a área do triângulo ABC é 36,6. Além disso, você também sabe que essa área é igual a
.
Sendo assim, temos que:
![\frac{1}{2}\sqrt{0^2 + 0^2 + [(6y-6) - (3x - 12)]^2} = 36,6 \frac{1}{2}\sqrt{0^2 + 0^2 + [(6y-6) - (3x - 12)]^2} = 36,6](/latexrender/pictures/35824b101ad2703700f4fe4831690814.png)


Desse modo, você precisa resolver o sistema:

Esse sistema pode ser dividido em dois casos.
Caso 1) 
 Caso 2)
Caso 2) 
Agora tente terminar o exercício.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [Geometria Analítica] Vértices do tetraedro
por -civil- » Qua Ago 17, 2011 22:38
- 1 Respostas
- 2574 Exibições
- Última mensagem por LuizAquino

Qua Ago 17, 2011 23:17
Geometria Analítica
-
- [Geometria Analítica] Encontrar os vértices do hexágono
 por -civil- » Qua Ago 10, 2011 16:51
por -civil- » Qua Ago 10, 2011 16:51
- 1 Respostas
- 2081 Exibições
- Última mensagem por LuizAquino

Sex Ago 12, 2011 12:44
Geometria Analítica
-
- [Geometria Analitica] Area de triangulo
por LucasSG » Sex Jun 21, 2013 10:57
- 1 Respostas
- 1507 Exibições
- Última mensagem por young_jedi

Sex Jun 21, 2013 21:23
Geometria Analítica
-
- geometria analitica (área do triângulo)
por romarioharket » Qua Nov 13, 2013 00:01
- 1 Respostas
- 3323 Exibições
- Última mensagem por e8group

Sex Nov 15, 2013 11:28
Geometria Analítica
-
- se um triangulo tem como vertices...
por willwgo » Seg Abr 18, 2011 17:44
- 2 Respostas
- 7915 Exibições
- Última mensagem por willwgo

Qua Abr 20, 2011 15:57
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
zig - Sex Set 23, 2011 13:57
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
Vennom - Sex Set 23, 2011 21:41
zig escreveu:![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)
Rpz, o negócio é o seguinte:
Quando você tem uma potência negativa, tu deve inverter a base dela. Por exemplo:

Então pense o seguinte: a fração geratriz de 0,05 é

, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
Veja:
![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
A raiz quadrada de vinte, você acha fácil, né?
Espero ter ajudado.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:23
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Assunto:
simplifiquei e achei...está certo?????????????
Autor:
fraol - Dom Dez 11, 2011 20:24
Nós podemos simplificar, um pouco,

da seguinte forma:

.
É isso.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


 .
.![\frac{1}{2}\sqrt{0^2 + 0^2 + [(6y-6) - (3x - 12)]^2} = 36,6 \frac{1}{2}\sqrt{0^2 + 0^2 + [(6y-6) - (3x - 12)]^2} = 36,6](/latexrender/pictures/35824b101ad2703700f4fe4831690814.png)




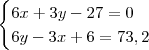

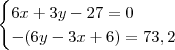

![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[5]}](/latexrender/pictures/19807748a214d3361336324f3e43ea9a.png)
![{(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}} {(0,05)}^{-\frac{1}{2}}=\frac{10}{\sqrt[2]{5}}](/latexrender/pictures/3d7908e5b4e397bf635b6546063d9130.png)

 , ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio.
, ou seja, 1 dividido por 20 é igual a 0.05 . Sendo assim, a função final é igual a vinte elevado à meio. ![{0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20} {0,05}^{-\frac{1}{2}} = {\frac{1}{20}}^{-\frac{1}{2}} = {\frac{20}{1}}^{\frac{1}{2}} = \sqrt[2]{20}](/latexrender/pictures/c0100c6f4d8bdbb7d54165e6be7aff04.png)
 da seguinte forma:
da seguinte forma: .
. da seguinte forma:
da seguinte forma: .
.