 por stuart clark » Seg Abr 09, 2012 12:16
por stuart clark » Seg Abr 09, 2012 12:16
If
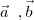
and
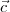
are three vectors such that
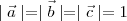
and
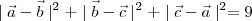
then
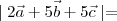
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por stuart clark » Seg Abr 09, 2012 12:19
por stuart clark » Seg Abr 09, 2012 12:19
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por stuart clark » Qua Abr 11, 2012 23:44
por stuart clark » Qua Abr 11, 2012 23:44
Thanks Moderator Got it
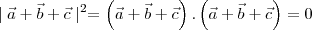
So
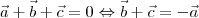
So
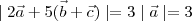
-
stuart clark
- Usuário Dedicado

-
- Mensagens: 34
- Registrado em: Sáb Mai 28, 2011 00:32
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por LuizAquino » Qui Abr 12, 2012 11:13
por LuizAquino » Qui Abr 12, 2012 11:13
stuart clark escreveu:Thanks Moderator Got it
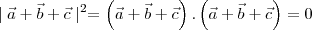
So
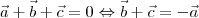
So
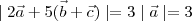
Ok.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
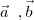 and
and 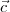 are three vectors such that
are three vectors such that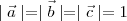 and
and 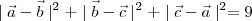
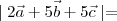

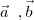 and
and 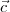 are three vectors such that
are three vectors such that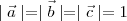 and
and 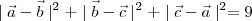
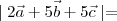

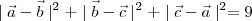
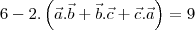
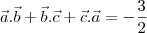

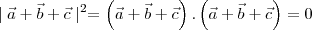
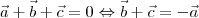
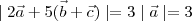




 , avisa que eu resolvo.
, avisa que eu resolvo.

