Verifique se em cada um dos itens abaixo o subconjunto W é um subespaço vetorial do espaço vetorial V. Caso não sejam especificadas, as operações são as usuais.
Então galera, o ítem que não consegui provar é o seguinte:

Se fosse p(0)=0 eu poderia usar as demonstrações usuais, só que assim eu já não sei... Alguém pode dar uma ajuda? Valeu



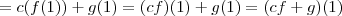 .
. e
e  pertencem ao espaço, sua avalição em zero é igual sua avalição em um.
pertencem ao espaço, sua avalição em zero é igual sua avalição em um.

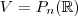 então
então 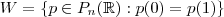 é subespaço.
é subespaço.![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)