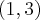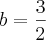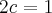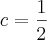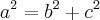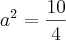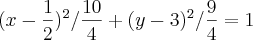por carmem » Seg Jun 01, 2009 16:21
por carmem » Seg Jun 01, 2009 16:21
Por favor, me ajude nestas questões:
1- encontre a equação da elipse satisfazendo as seguintes condições;
a) (0,3) e (1,3) são os focos e o eixo menor é 3
b) os quato vértices são: (2,1), (6,1), (3,6) e (3,-4).
obrigada
carmem
Mensagens: 3
Data de registro: Ter Mai 12, 2009 23:25
Formação Escolar: SUPLETIVO
Área/Curso: matematica
Andamento: cursando
-
carmem
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Mai 12, 2009 23:25
- Formação Escolar: SUPLETIVO
- Área/Curso: matematica
- Andamento: cursando
 por Cleyson007 » Seg Jun 01, 2009 19:47
por Cleyson007 » Seg Jun 01, 2009 19:47
Boa noite Carmem.
Seja bem vinda ao Ajuda Matemática.
Não sei se você tem o gabarito, mas se tiver, é importante colocá-lo, a fim de facilitar a vida de quem se dispõe a ajudá-la.
Segue resolução da letra a:
a) Equação reduzida da elipse com centro fora da origem dos eixos coordenados.
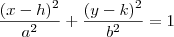
Temos:
Centro da elipse
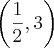
Dois focos:
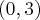
e
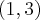
Quanto ao eixo menor:

Logo:
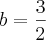
Quanto a distância focal:
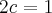
Logo:
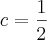
Lembrando que:
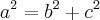
Logo:
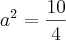
Daí:
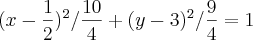
Portanto:

Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por carmem » Seg Jun 01, 2009 22:08
por carmem » Seg Jun 01, 2009 22:08
Oi Cleyson,
obrigada pela resolução da letra. Não tenho o gabarito infelizmente.
Mas tinha tentado resolve-la e não obtive sucesso.
E a letra b)? Como eu encontro a equação com os dados das quatro vertices?
Carminha
-
carmem
- Usuário Ativo

-
- Mensagens: 11
- Registrado em: Ter Mai 12, 2009 23:25
- Formação Escolar: SUPLETIVO
- Área/Curso: matematica
- Andamento: cursando
 por Cleyson007 » Sex Jun 05, 2009 12:54
por Cleyson007 » Sex Jun 05, 2009 12:54
Boa tarde Carmem!
Carmem, com relação a letra b, não estou conseguindo desenhar a elipse com os vértices que você descreveu.
Posso apresentar o meu modo de resolvê-lo?
Até mais.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Elipse
por lucas1365 » Sex Jul 03, 2009 21:30
- 0 Respostas
- 1788 Exibições
- Última mensagem por lucas1365

Sex Jul 03, 2009 21:30
Geometria Analítica
-
- Elipse
por Siax » Sex Jul 10, 2009 00:03
- 0 Respostas
- 1775 Exibições
- Última mensagem por Siax

Sex Jul 10, 2009 00:03
Geometria Analítica
-
- Elipse
por Claudin » Dom Mai 20, 2012 16:46
- 14 Respostas
- 6148 Exibições
- Última mensagem por Claudin

Dom Mai 20, 2012 20:40
Geometria Analítica
-
- Elipse
por Claudin » Dom Mai 20, 2012 18:50
- 2 Respostas
- 1605 Exibições
- Última mensagem por Claudin

Qui Mai 24, 2012 02:55
Geometria Analítica
-
- Elipse
por Claudin » Dom Mai 20, 2012 20:07
- 2 Respostas
- 1420 Exibições
- Última mensagem por Claudin

Ter Jun 12, 2012 20:29
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.


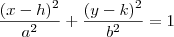
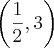
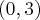 e
e