Dúvidas de Geometria analítica

por **Priscila_moraes** » Ter Nov 15, 2011 19:35

oi pessoal como resolvo essa questão 16y²=4x²+z² acredito que seja a equação do hiperboloide de uma folha da certo?

por **LuizAquino** » Qua Nov 16, 2011 17:05

Priscila_moraes escreveu:oi pessoal como resolvo essa questão 16y²=4x²+z²

Você deve analisar as curvas de nível.

Caso 1) x = k.

Se k = 0, então temos as retas z = 4y e z = -4y.

Se k não nulo, então temos as hipérboles $\frac{y^2}{\frac{4k^2}{16}} - \frac{z^2}{4k^2} = 1$ .

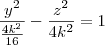
: caso1.png (48.54 KiB) Exibido 1233 vezes

Caso 2) y = k.

Se k = 0, então temos apenas o ponto (0, 0, 0).

Se k não nulo, então temos as elipses $\frac{x^2}{\frac{16k^2}{4}} + \frac{z^2}{16k^2} = 1$ .

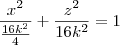
: caso2.png (18.66 KiB) Exibido 1233 vezes

Caso 3) z = k.

Se k = 0, então temos as retas y = x/2 e y = -x/2.

Se k não nulo, então temos as hipérboles $\frac{y^2}{\frac{k^2}{16}} - \frac{x^2}{\frac{k^2}{4}} = 1$ .

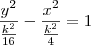
: caso3.png (49.33 KiB) Exibido 1233 vezes

Após analisar as curvas de nível, você pode fazer um esboço da superfície.

Priscila_moraes escreveu:acredito que seja a equação do hiperboloide de uma folha da certo?

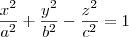
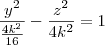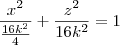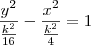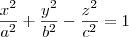Não. Lembre-se que um hiperboloide de uma folha tem uma equação da forma $\frac{x^2}{a^2} + \frac{y^2}{b^2} - \frac{z^2}{c^2}=1$ .

Dúvidas de Geometria analítica

Dúvidas de Geometria analítica

Dúvidas de Geometria analítica

Re: Dúvidas de Geometria analítica

Quem está online