[Geometria] Ângulos.

[Lucas Ponte]

Não sei se ta na área certa, não sei se to postando nem no fórum certo. '-'
PS: Sou aluno, não achei nada aqui em relação à aluno e não encontrei outro site qual aparenta ter membros experientes..
Enfim.. Estou com um ângulo aqui que não consigo identificado o valor de "alfa", o qual meu professor
ainda não explicou e provavelmente irá passar de novo uma questão do tipo, já que ninguém conseguiu resolver

Já tentei diversas coisas, como multiplicar em X, somar lado com lado e saber resultado de x ou y..
não me restam mais alternativas para resolver isso, só se eu inventar uma. -rs

A questão seria, qual o valor que alfa assume na representação?

Se bugar: http://i.imgur.com/VCLEB.jpg


Alguém pode ajudar? Agradeço.

[LuizAquino]

Qual o valor que alfa assume na representação?

VCLEB.jpg (10.5 KiB) Exibido 1101 vezes

Os ângulos x + y e 4x - 2y são suplementares. Sendo assim, note que:

(x + y) + (4x - 2y) = 180°

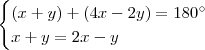
Já os ângulos x + y e 2x - y são opostos pelo vértice. Sendo assim, note que:

x + y = 2x - y

Com essas duas equações, você pode montar o sistema:



Resolvendo esse sistema, você obtém x = 40° e y = 20°.

Agora note que os ângulos e 4x - 2y são opostos pelo vértice. Sendo assim, temos que: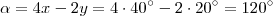

.