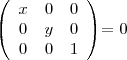18 - 30) O plano
 contém r : x - y = x + z - 1 = 0 e determina, com os planos coordenados, um tetraedro de volume
contém r : x - y = x + z - 1 = 0 e determina, com os planos coordenados, um tetraedro de volume  . Supondo que estamos num sistema ortogonal, obtenha os vértices de tetraedro e uma equação geral de
. Supondo que estamos num sistema ortogonal, obtenha os vértices de tetraedro e uma equação geral de  .
.Volume do tetraedro =

Consideramos que A está no eixo x, B está no eixo y e C está no eixo z.
A = (x,0,0), B = (0,y,0), C = (0,0,z)
Percebemos que C
 r, então C = (0,0,1)
r, então C = (0,0,1)![\frac{1}{6}[\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}] \frac{1}{6}[\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}]](/latexrender/pictures/6126faa522fa196b380f6dbc39760788.png) =
= 
![[\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}] [\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}]](/latexrender/pictures/b58c25e1dfbbf5b50e2909b7d9a2b924.png) =
= 
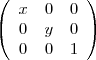 = 0
= 0(Na verdade isso é um determinante, só que eu não sei como colocar em Latex)
|xy| =

Como r
 , então {
, então {![[\overrightarrow{CA}, \overrightarrow{CB}, \overrightarrow{r}] [\overrightarrow{CA}, \overrightarrow{CB}, \overrightarrow{r}]](/latexrender/pictures/cb819072c20d67c157c203769b01ec95.png) } é LI
} é LI = (x, 0, -1),
= (x, 0, -1), 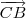 = (0, y, -1),
= (0, y, -1),  = (1, 1, -1)
= (1, 1, -1)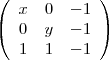 = 0
= 0-xy + x + y = 0
Como |xy| =
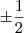
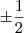 + x + y = 0
+ x + y = 0x + y =
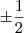
Para x + y =
 e
e 
Sistema impossível
Para x + y =
 e
e 
y' = 1, x' =
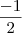
y" =
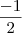 , x" = -1
, x" = -1Para x + y =
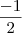 e
e 
Sistema impossível
Para x + y =
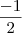 e
e 
y' = -1, x' =

y" =
 , x" = 1
, x" = 1Sem procurar ainda a equação da reta, eu encontrei quatro soluções diferentes. Mas há apenas duas soluções corretas do exercício:
y' = -1, x' =

y" =
 , x" = 1
, x" = 1Por que as outras duas estão erradas?