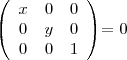por -civil- » Qua Ago 17, 2011 22:38
por -civil- » Qua Ago 17, 2011 22:38
Boulos - 3a. ed.
18 - 30) O plano  contém r : x - y = x + z - 1 = 0 e determina, com os planos coordenados, um tetraedro de volume
contém r : x - y = x + z - 1 = 0 e determina, com os planos coordenados, um tetraedro de volume  . Supondo que estamos num sistema ortogonal, obtenha os vértices de tetraedro e uma equação geral de
. Supondo que estamos num sistema ortogonal, obtenha os vértices de tetraedro e uma equação geral de  .
.Volume do tetraedro =

Consideramos que A está no eixo x, B está no eixo y e C está no eixo z.
A = (x,0,0), B = (0,y,0), C = (0,0,z)
Percebemos que C

r, então C = (0,0,1)
![\frac{1}{6}[\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}] \frac{1}{6}[\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}]](/latexrender/pictures/6126faa522fa196b380f6dbc39760788.png)
=

![[\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}] [\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}]](/latexrender/pictures/b58c25e1dfbbf5b50e2909b7d9a2b924.png)
=

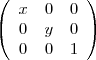
= 0
(Na verdade isso é um determinante, só que eu não sei como colocar em Latex)
|xy| =

Como r

, então {
![[\overrightarrow{CA}, \overrightarrow{CB}, \overrightarrow{r}] [\overrightarrow{CA}, \overrightarrow{CB}, \overrightarrow{r}]](/latexrender/pictures/cb819072c20d67c157c203769b01ec95.png)
} é LI

= (x, 0, -1),
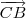
= (0, y, -1),

= (1, 1, -1)
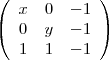
= 0
-xy + x + y = 0
Como |xy| =
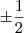
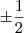
+ x + y = 0
x + y =
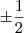
Para x + y =

e

Sistema impossível
Para x + y =

e

y' = 1, x' =
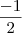
y" =
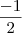
, x" = -1
Para x + y =
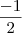
e

Sistema impossível
Para x + y =
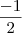
e

y' = -1, x' =

y" =

, x" = 1
Sem procurar ainda a equação da reta, eu encontrei quatro soluções diferentes. Mas há apenas duas soluções corretas do exercício:
y' = -1, x' =

y" =

, x" = 1
Por que as outras duas estão erradas?
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Qua Ago 17, 2011 23:17
por LuizAquino » Qua Ago 17, 2011 23:17
-civil- escreveu:Por que as outras duas estão erradas?
Você está fazendo quatro casos, quando na verdade só há dois.
Da equação |xy| = 1/2, temos dois casos:
(i) xy = 1/2
(ii) xy = -1/2
Quando o caso (i) acontecer, a equação |xy| + x + y = 0 é a mesma que x + y = -1/2.
Por outro lado, quando o caso (ii) acontecer, a equação |xy| + x + y = 0 é a mesma que x + y = 1/2.
-civil- escreveu: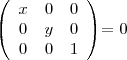
(Na verdade isso é um determinante, só que eu não sei como colocar em Latex)
Basta usar o comando:
- Código: Selecionar todos
[tex]
\begin{vmatrix}
x & 0 & 0 \\
0 & y & 0 \\
0 & 0 & 1
\end{vmatrix}
[/tex]
O resultado desse comando é:

-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Geometria analitica - vertices do triangulo
por Dayannearaujo » Qui Abr 19, 2012 17:21
- 1 Respostas
- 2320 Exibições
- Última mensagem por LuizAquino

Sex Abr 20, 2012 00:07
Geometria Analítica
-
- [Geometria Analítica] Encontrar os vértices do hexágono
 por -civil- » Qua Ago 10, 2011 16:51
por -civil- » Qua Ago 10, 2011 16:51
- 1 Respostas
- 2087 Exibições
- Última mensagem por LuizAquino

Sex Ago 12, 2011 12:44
Geometria Analítica
-
- Vértices do tetraedro e equação geral do plano
por -civil- » Qua Jun 15, 2011 23:04
- 1 Respostas
- 4015 Exibições
- Última mensagem por LuizAquino

Qui Jun 16, 2011 17:57
Geometria Analítica
-
- Tetraedro - Motivo que os vértices formam base e coordenadas
 por rochadapesada » Sáb Dez 14, 2013 21:29
por rochadapesada » Sáb Dez 14, 2013 21:29
- 7 Respostas
- 3214 Exibições
- Última mensagem por Russman

Dom Dez 15, 2013 14:18
Geometria Analítica
-
- [Geometria espacial] Volume de tetraedro
 por rochadapesada » Seg Abr 08, 2013 21:48
por rochadapesada » Seg Abr 08, 2013 21:48
- 6 Respostas
- 6201 Exibições
- Última mensagem por rochadapesada

Qua Abr 10, 2013 21:23
Geometria Espacial
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 contém r : x - y = x + z - 1 = 0 e determina, com os planos coordenados, um tetraedro de volume
contém r : x - y = x + z - 1 = 0 e determina, com os planos coordenados, um tetraedro de volume  . Supondo que estamos num sistema ortogonal, obtenha os vértices de tetraedro e uma equação geral de
. Supondo que estamos num sistema ortogonal, obtenha os vértices de tetraedro e uma equação geral de  .
.
 r, então C = (0,0,1)
r, então C = (0,0,1)![\frac{1}{6}[\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}] \frac{1}{6}[\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}]](/latexrender/pictures/6126faa522fa196b380f6dbc39760788.png) =
= 
![[\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}] [\overrightarrow{OA}, \overrightarrow{OB}, \overrightarrow{OC}]](/latexrender/pictures/b58c25e1dfbbf5b50e2909b7d9a2b924.png) =
= 
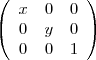 = 0
= 0
 , então {
, então {![[\overrightarrow{CA}, \overrightarrow{CB}, \overrightarrow{r}] [\overrightarrow{CA}, \overrightarrow{CB}, \overrightarrow{r}]](/latexrender/pictures/cb819072c20d67c157c203769b01ec95.png) } é LI
} é LI = (x, 0, -1),
= (x, 0, -1), 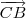 = (0, y, -1),
= (0, y, -1),  = (1, 1, -1)
= (1, 1, -1)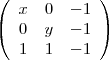 = 0
= 0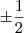
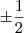 + x + y = 0
+ x + y = 0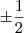
 e
e 
 e
e 
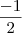
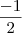 , x" = -1
, x" = -1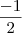 e
e 
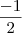 e
e 

 , x" = 1
, x" = 1
 , x" = 1
, x" = 1