18-15) Um hexágono regular contido em
 : x + y + z - 3 = 0 tem centro H = (1,1,1) e seu lado mede
: x + y + z - 3 = 0 tem centro H = (1,1,1) e seu lado mede  (SO). Determine seus vértices, sabendo que dois deles pertencem a r: X = (1,1,1) +
(SO). Determine seus vértices, sabendo que dois deles pertencem a r: X = (1,1,1) +  (1,0,-1).
(1,0,-1).dist(A,H) =

A = ( 1 +
 , 1, 1 -
, 1, 1 -  )
)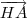 = (
= ( , 0,
, 0, 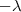 )
)||
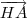 || =
|| = 
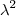 +
+ 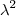 = 2
= 2 =
= 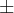 1
1A = (2,1,0) e D = (0,1,2)
Como faço agora para encontrar os outros pontos?



![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png)
 e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)