 por -civil- » Qui Jul 07, 2011 23:26
por -civil- » Qui Jul 07, 2011 23:26
-
-civil-
- Usuário Dedicado

-
- Mensagens: 47
- Registrado em: Sex Abr 22, 2011 12:31
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia Civil
- Andamento: cursando
 por LuizAquino » Sex Jul 08, 2011 11:22
por LuizAquino » Sex Jul 08, 2011 11:22
-civil- escreveu:Para mim isso é uma regra dada pelo Boulos, mas como provar?
Para provar use a dica fornecida!
Dada um ponto

do plano e um vetor

paralelo ao plano, o ponto

também pertence ao plano. Isso significa que tanto
A quanto
B atendem a equação
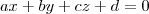
.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Posição relativa de retas e planos
 por hygorvv » Qua Jul 25, 2012 12:45
por hygorvv » Qua Jul 25, 2012 12:45
- 4 Respostas
- 5896 Exibições
- Última mensagem por hygorvv

Qui Jul 26, 2012 15:50
Geometria Analítica
-
- posição relativa entre os planos
por Ana Maria da Silva » Ter Jun 04, 2013 10:38
- 2 Respostas
- 3562 Exibições
- Última mensagem por Ana Maria da Silva

Ter Jun 04, 2013 20:31
Geometria Analítica
-
- posicao relativa de retas e planos
por Livingstone » Sex Dez 12, 2014 15:31
- 0 Respostas
- 1506 Exibições
- Última mensagem por Livingstone

Sex Dez 12, 2014 15:31
Geometria Analítica
-
- [Posição relativa de retas e planos - Geometria Analítica]
por Gustavo195 » Dom Abr 07, 2013 16:34
- 0 Respostas
- 2548 Exibições
- Última mensagem por Gustavo195

Dom Abr 07, 2013 16:34
Geometria Analítica
-
- posição relativa entre as retas r e pi
por Ana Maria da Silva » Qua Jun 05, 2013 11:55
- 0 Respostas
- 1344 Exibições
- Última mensagem por Ana Maria da Silva

Qua Jun 05, 2013 11:55
Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
[calculo] derivada
Autor:
beel - Seg Out 24, 2011 16:59
Para derivar a função
(16-2x)(21-x).x
como é melhor fazer?
derivar primeiro sei la, ((16-2x)(21-x))' achar o resultado (y)
e depois achar (y.x)' ?
Assunto:
[calculo] derivada
Autor:
MarceloFantini - Seg Out 24, 2011 17:15
Você poderia fazer a distributiva e derivar como um polinômio comum.
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:26
Funciona da mesma forma que derivada de x.y.z, ou seja, x'.y.z+x.y'.z+x.y.z' substitui cada expressão pelas variáveis e x',y' e z' é derivada de cada um
Assunto:
[calculo] derivada
Autor:
wellersonobelix - Dom Mai 31, 2015 17:31
derivada de (16-2x)=-2
derivada de (21-x)=-1
derivada de x=1
derivada de (16-2x)(21-x)x=-2.(21-x)x+(-1).(16-2x)x +1.(16-2x)(21-x)
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e
e  = (m, n, p). Então,
= (m, n, p). Então,  é paralelo a
é paralelo a  se, e somente se, am + bn + cp = 0. Dica: considere um ponto A
se, e somente se, am + bn + cp = 0. Dica: considere um ponto A  e tome um ponto B = A +
e tome um ponto B = A + 

 e
e  = (m, n, p). Então,
= (m, n, p). Então,  é paralelo a
é paralelo a  se, e somente se, am + bn + cp = 0. Dica: considere um ponto A
se, e somente se, am + bn + cp = 0. Dica: considere um ponto A  e tome um ponto B = A +
e tome um ponto B = A + 

 do plano e um vetor
do plano e um vetor  paralelo ao plano, o ponto
paralelo ao plano, o ponto  também pertence ao plano. Isso significa que tanto A quanto B atendem a equação
também pertence ao plano. Isso significa que tanto A quanto B atendem a equação 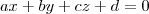 .
.