Vértices do tetraedro e equação geral do plano

[-civil-]

O plano contém
r : x - y = 0
x + z - 1 = 0
e determina, com os planos coordenados, um tetraedro de volume . Supondo que estamos num sistema ortogonal, obtenha os vértices do tetraedro e uma equação geral de .

O volume do tetraedro é 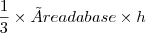= 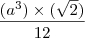, sendo "a" a aresta do tetraedro

O volume dado é . Daí, igualando as equações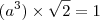

Eu transformei a equação de r para a forma vetorial e considerando x=, obtive:
r: X = (0,0,1) + (1,1,-1)

Eu considerei o mesmo ponto e vetor diretor da reta r, como o ponto e um dos vetores diretores de mas eu preciso também de mais um vetor de . Não sei como prosseguir.

Agradeço pela ajuda

[LuizAquino]

O tetraedro do exercício não é regular (isto é, não é formado por triângulos equiláteros). Portanto, você não pode usar a fórmula para o volume como se todas as arestas fossem iguais.

Aqui vão três dicas:
(i) se , e 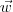representam as arestas partindo de um mesmo vértice do tetraedro, então o seu volume é dado por .
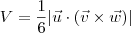(ii) um dos vértices do tetraedro é a origem do sistema de coordenadas.
(iii) um dos vértices do tetraedro coincide com a interseção de r com o eixo z.