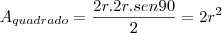por stanley tiago » Seg Mai 02, 2011 16:35
por stanley tiago » Seg Mai 02, 2011 16:35
determine a area das superfícies assinaladas da figura:
a) ABCD é um quadrado , e r =
![8 \sqrt[]{2} 8 \sqrt[]{2}](/latexrender/pictures/68ec525367b08678e151e9883e3334c9.png)
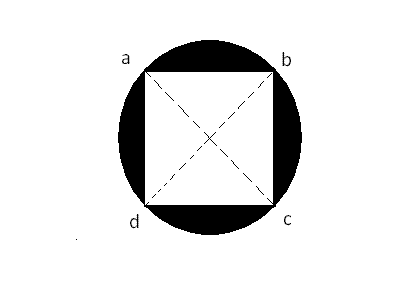
- sfds.GIF (2.66 KiB) Exibido 2438 vezes
Eu tentei de alguma formas aqui só q nao deu muito certo

--
![r=8\sqrt[]{3} r=8\sqrt[]{3}](/latexrender/pictures/e963174c3c9c078bf1063cb489ebfd9f.png)
--
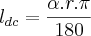
então
![{l}_{dc}= \frac{90.8\sqrt[]{2}.\pi}{180} {l}_{dc}= \frac{90.8\sqrt[]{2}.\pi}{180}](/latexrender/pictures/e9dc9a171ff8bc0ae0e4bc92e5be16c0.png)
--
![{l}_{dc}= 4\pi\sqrt[]{2} {l}_{dc}= 4\pi\sqrt[]{2}](/latexrender/pictures/9b840bdf4e4cda019f61e332b46aae01.png)

--
![{A}_{s}= \frac{4\pi\sqrt[]{2}.8\sqrt[]{2}}{2} {A}_{s}= \frac{4\pi\sqrt[]{2}.8\sqrt[]{2}}{2}](/latexrender/pictures/6df638a8468d9af2759a4ae6836ef3e1.png)
--
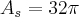
Então pessual foi até aqui que eu consegui tirar do exercício , apartir daqui eu nao sei o que fazer !
Ah , a resposta certa é 145,92 cm²
-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por TheoFerraz » Seg Mai 02, 2011 17:02
por TheoFerraz » Seg Mai 02, 2011 17:02
Pense o seguinte.
O diametro da circunferencia é a diagonal do quadrado.
A diagonal dum quadrado de lado

é sempre
![\alpha\sqrt[]{2} \alpha\sqrt[]{2}](/latexrender/pictures/4fff6a7637f05449fed26931624c3004.png)
.
No seu caso. a diagonal é duas vezes o raio (diametro) entao fica que o lado do quadrado é
![\alpha\sqrt[]{2}} = 2\times8\sqrt[]{2} \alpha\sqrt[]{2}} = 2\times8\sqrt[]{2}](/latexrender/pictures/9bcff7fe80732bcb4801ce59ea1b33f7.png)

Dai voce percebe que seu quadrado tem lado 16.
Se voce quer a area da parte preta na figura. é simples
Area da circunferencia - area do quadrado = area desejada
Portanto:
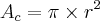
e

Ai voce faz a conta pans, só não vou falar muito pq acabei de me tocar que nao sei direito o que o problema pede, se for a area preta entao faça isso,

Mas de qualquer jeito, use aquela jogada da diagonal do quadrado ser sempre
![\alpha\sqrt[]{2} \alpha\sqrt[]{2}](/latexrender/pictures/4fff6a7637f05449fed26931624c3004.png)
. E do diametro ser a diagonal do quadrado. Saindo dai vc tem informação até demais
Espero ter ajudado, Abraço
-
TheoFerraz
- Colaborador Voluntário

-
- Mensagens: 107
- Registrado em: Qua Abr 13, 2011 19:23
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Bacharelado em Física
- Andamento: cursando
 por stanley tiago » Seg Mai 02, 2011 17:22
por stanley tiago » Seg Mai 02, 2011 17:22
É deu certo sim mlk , é isso mesmo
TheoFerraz escreveu:
vlw obrigado pela ajuda

-
stanley tiago
- Usuário Parceiro

-
- Mensagens: 57
- Registrado em: Seg Jan 17, 2011 14:23
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por FilipeCaceres » Seg Mai 02, 2011 19:51
por FilipeCaceres » Seg Mai 02, 2011 19:51
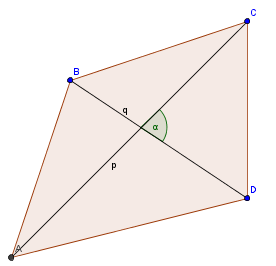
- quadrilatero.png (6.35 KiB) Exibido 2427 vezes
Só para complementar.
Dado um quadrilátero qualquer, podemos descobrir qual a sua área sabendo o valor das diagonais e o ângulo entre elas.

No exercício temos um quadrado, e portanto as diagonais são iguais e com valor
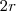
,pois está inscrita em uma circunferência, e o ângulo entre elas é de

, desta forma temos,
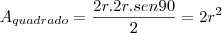
O resto é semelhante,



Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
Voltar para Geometria Analítica
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Setor circular
 por DanielFerreira » Sex Mar 04, 2011 11:08
por DanielFerreira » Sex Mar 04, 2011 11:08
- 1 Respostas
- 3959 Exibições
- Última mensagem por LuizAquino

Sex Mar 04, 2011 12:08
Geometria Plana
-
- Setor Circular
 por Arkanus Darondra » Qua Fev 01, 2012 18:42
por Arkanus Darondra » Qua Fev 01, 2012 18:42
- 6 Respostas
- 5746 Exibições
- Última mensagem por Arkanus Darondra

Dom Fev 05, 2012 09:20
Geometria Espacial
-
- Permutação circular
por anfran1 » Dom Nov 17, 2013 10:53
- 0 Respostas
- 1081 Exibições
- Última mensagem por anfran1

Dom Nov 17, 2013 10:53
Análise Combinatória
-
- pista circular
por adauto martins » Seg Set 29, 2014 15:45
- 1 Respostas
- 1164 Exibições
- Última mensagem por adauto martins

Sex Jul 22, 2016 17:04
Cálculo: Limites, Derivadas e Integrais
-
- Calculo circular
por lucastrmendes » Sex Mai 08, 2015 16:07
- 0 Respostas
- 2245 Exibições
- Última mensagem por lucastrmendes

Sex Mai 08, 2015 16:07
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 12:41
pessoal eu achei como resultado 180 toneladas,entretanto sei que a questão está erra pela lógica e a resposta correta segundo o gabarito é 1.800 toneladas.
me explique onde eu estou pecando na questão. resolva explicando.
78 – ( CEFET – 1993 ) Os desabamentos, em sua maioria, são causados por grande acúmulo de lixo nas encostas dos morros. Se 10 pessoas retiram 135 toneladas de lixo em 9 dias, quantas toneladas serão retiradas por 40 pessoas em 30 dias ?
Assunto:
dúvida em uma questão em regra de 3!
Autor:
Douglasm - Qui Jul 01, 2010 13:16
Observe o raciocínio:
10 pessoas - 9 dias - 135 toneladas
1 pessoa - 9 dias - 13,5 toneladas
1 pessoa - 1 dia - 1,5 toneladas
40 pessoas - 1 dia - 60 toneladas
40 pessoas - 30 dias - 1800 toneladas
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:18
pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
Assunto:
dúvida em uma questão em regra de 3!
Autor:
leandro moraes - Qui Jul 01, 2010 13:21
leandro moraes escreveu:pessoal já achei a resposta. o meu erro foi bobo rsrsrrs errei em uma continha de multiplicação, é mole rsrsrsr mas felizmente consegui.
valeu meu camarada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![8 \sqrt[]{2} 8 \sqrt[]{2}](/latexrender/pictures/68ec525367b08678e151e9883e3334c9.png)
 --
-- ![r=8\sqrt[]{3} r=8\sqrt[]{3}](/latexrender/pictures/e963174c3c9c078bf1063cb489ebfd9f.png) --
-- 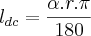
![{l}_{dc}= \frac{90.8\sqrt[]{2}.\pi}{180} {l}_{dc}= \frac{90.8\sqrt[]{2}.\pi}{180}](/latexrender/pictures/e9dc9a171ff8bc0ae0e4bc92e5be16c0.png) --
-- ![{l}_{dc}= 4\pi\sqrt[]{2} {l}_{dc}= 4\pi\sqrt[]{2}](/latexrender/pictures/9b840bdf4e4cda019f61e332b46aae01.png)
 --
-- ![{A}_{s}= \frac{4\pi\sqrt[]{2}.8\sqrt[]{2}}{2} {A}_{s}= \frac{4\pi\sqrt[]{2}.8\sqrt[]{2}}{2}](/latexrender/pictures/6df638a8468d9af2759a4ae6836ef3e1.png) --
-- 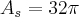


 é sempre
é sempre ![\alpha\sqrt[]{2} \alpha\sqrt[]{2}](/latexrender/pictures/4fff6a7637f05449fed26931624c3004.png) .
.![\alpha\sqrt[]{2}} = 2\times8\sqrt[]{2} \alpha\sqrt[]{2}} = 2\times8\sqrt[]{2}](/latexrender/pictures/9bcff7fe80732bcb4801ce59ea1b33f7.png)

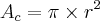





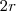 ,pois está inscrita em uma circunferência, e o ângulo entre elas é de
,pois está inscrita em uma circunferência, e o ângulo entre elas é de  , desta forma temos,
, desta forma temos,