Olá
jefferson2z, boas-vindas!
O enunciado pode sim postar, mas a "regra" é complementar comentando as tentativas e especificando as dúvidas.
Vou comentar as etapas de uma solução para você tentar... Antes, o foco do problema: encontrar as coordenadas do ponto C.
Plano para determinar o ponto C:
-conforme figura, construa a bissetriz

que passará pelo ponto médio

do segmento
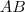
;
-obtenha as coordenadas do ponto

;
-determine a equação reduzida da reta

(que contém o segmento
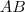
da base do triângulo) e anote seu coeficiente angular (ou apenas calcule o coeficiente angular);
-como

é perpendicular à

e passa por

, determine também sua equação;
-determine a intersecção entre

e

para obter o ponto

;
Finalizando:
-com o ponto

, será imediato determinar a equação da reta

, pois já temos

;
-deixe a equação de

na forma reduzida para destacar o coeficiente angular procurado;
-ou ainda, determine diretamente apenas o coeficiente angular de

.
Espero ter ajudado.
Comente as dúvidas. Bons estudos!



 que passará pelo ponto médio
que passará pelo ponto médio  do segmento
do segmento 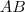 ;
; (que contém o segmento
(que contém o segmento  e
e  ;
; , pois já temos
, pois já temos  ;
;
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  por
por  .
.
