a) R = 8 cm
d= 2.r -------- d = 16 --------- d = x+m ----------- x=16-m
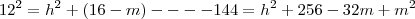
bom pessoal isso foi tudo q eu consegui fazer , conto com a colaboraçao de vcs !

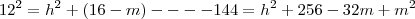







Voltar para Geometria Analítica
Usuários navegando neste fórum: Nenhum usuário registrado e 4 visitantes

 .
.
 :
: