drakonifor escreveu:(ii) : (x1,y1) + (x2,y2) (tal que x+y= 0) = (x1+x2, y1+y2);
Como (x y) tem de ser 0 significa que o X e o Y são 0 o que faz com que (x1+x2, y1+y2) seja 0 logo tambem está provado.
Você está confundindo tudo! Se (x, y) está em
S isso significa que
x+y=0 e não que "x e o y são 0". Por exemplo, (1, -1) está em
S, pois
1 + (-1) = 0, mas nem x e nem y são 0.
O que você tem que provar é que se (x1, y1) e (x2, y2) estão em
S, então (x1+x2, y1+y2) também está em
S. Ou seja, você tem que provar que
(x1+x2)+(y1+y2)=0.
drakonifor escreveu:(III) : Qualquer valor multiplicado por 0 dá 0 logo a(x,y) será sempre igual a 0 por isso está provado que é subespaço.
Aqui você não justificou o que se quer! E ainda continua confundindo tudo!
O que você tem que provar é que se (x, y) está em
S, então (kx, ky) também está em
S. Ou seja, você tem que provar que
kx+ky=0.



 .
. sobre o corpo
sobre o corpo  . Seja o subconjunto
. Seja o subconjunto  de
de  . Sendo assim,
. Sendo assim, 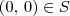
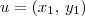 e
e 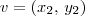 pertencentes a
pertencentes a  . Agora, será que
. Agora, será que 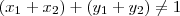 ? Não necessariamente! Por exemplo, temos que
? Não necessariamente! Por exemplo, temos que 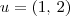 e
e  pertencem a
pertencem a  e
e 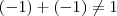 . Porém,
. Porém,  e portanto
e portanto  . Isso significa que
. Isso significa que 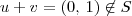 .
.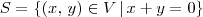 é subespaço de
é subespaço de 

 .
.



