 por Louis » Qua Jul 11, 2012 00:58
por Louis » Qua Jul 11, 2012 00:58
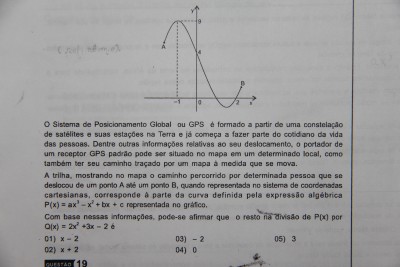
Devo relacionar os valores de x do sistema de coordenadas com a expressão algébrica P(x), realizando uma substituição?
Obrigado.
- Anexos
-
-
Louis
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Jul 09, 2012 17:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Qua Jul 11, 2012 02:17
por Russman » Qua Jul 11, 2012 02:17
Sim!
Observe que o problema fornece a forma da equação do gráfico e 3 pontos.
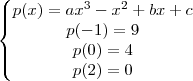
Assim,
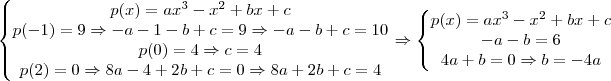
e, portanto,

.
Visto isso, a sua função é
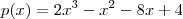
.
Agora, basta dividir por

.
Editado pela última vez por
Russman em Qua Jul 11, 2012 18:03, em um total de 1 vez.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
 por Louis » Qua Jul 11, 2012 12:36
por Louis » Qua Jul 11, 2012 12:36
Tentei aplicar Ruffini na divisão de polinômios, para isso encontrei o valor de cada x na expressão do Q(x). Penso que Ruffini não se aplicaria nesse caso, certo? Isso porque encontrei dois valores para o resto, ou seja, apliquei Ruffini para cada x que calculei. Não consegui por este método e então optei pelo tradicional de divisão, mas estou encontrando como resto 16x e o gabarito afirma que o valor do resto é 0.

-
Louis
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Jul 09, 2012 17:48
- Formação Escolar: GRADUAÇÃO
- Andamento: cursando
 por Russman » Qua Jul 11, 2012 18:04
por Russman » Qua Jul 11, 2012 18:04
eu calculo
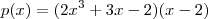
.
Portanto o resto da divisão tem de ser

.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Divisão de polinômios
por manuoliveira » Dom Nov 14, 2010 14:00
- 1 Respostas
- 2589 Exibições
- Última mensagem por VtinxD

Seg Nov 15, 2010 01:13
Polinômios
-
- Divisão de Polinômios
por -civil- » Seg Mai 30, 2011 20:31
- 3 Respostas
- 2424 Exibições
- Última mensagem por -civil-

Seg Mai 30, 2011 21:20
Cálculo: Limites, Derivadas e Integrais
-
- divisão de polinomios
por theSinister » Seg Mai 23, 2011 17:11
- 6 Respostas
- 3897 Exibições
- Última mensagem por theSinister

Seg Mai 23, 2011 22:34
Álgebra Elementar
-
- Divisão de Polinômios
por Claudin » Qua Ago 03, 2011 20:25
- 3 Respostas
- 2176 Exibições
- Última mensagem por Claudin

Qui Ago 04, 2011 15:46
Polinômios
-
- Divisão de polinômios
por Gaules » Qua Out 19, 2011 16:47
- 0 Respostas
- 1410 Exibições
- Última mensagem por Gaules

Qua Out 19, 2011 16:47
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Unesp - 95 Números Complexos
Autor:
Alucard014 - Dom Ago 01, 2010 18:22
(UNESP - 95) Seja L o Afixo de um Número complexo

em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
Assunto:
Unesp - 95 Números Complexos
Autor:
MarceloFantini - Qui Ago 05, 2010 17:27
Seja

o ângulo entre o eixo horizontal e o afixo

. O triângulo é retângulo com catetos

e

, tal que

. Seja

o ângulo complementar. Então

. Como

, o ângulo que o afixo

formará com a horizontal será

, mas negativo pois tem de ser no quarto quadrante. Se

, então

. Como módulo é um:

.
Logo, o afixo é

.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.



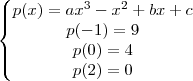
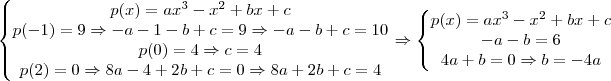
 .
.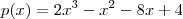 .
. .
.



 em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto.
em um sistema de coordenadas cartesianas xOy. Determine o número complexo b , de módulo igual a 1 , cujo afixo M pertence ao quarto quadrante e é tal que o ângulo LÔM é reto. o ângulo entre o eixo horizontal e o afixo
o ângulo entre o eixo horizontal e o afixo  . O triângulo é retângulo com catetos
. O triângulo é retângulo com catetos  e
e  , tal que
, tal que  . Seja
. Seja  o ângulo complementar. Então
o ângulo complementar. Então  . Como
. Como  , o ângulo que o afixo
, o ângulo que o afixo  formará com a horizontal será
formará com a horizontal será  , mas negativo pois tem de ser no quarto quadrante. Se
, mas negativo pois tem de ser no quarto quadrante. Se  , então
, então  . Como módulo é um:
. Como módulo é um:  .
. .
.