Chequei até este ponto:




bira19 escreveu:Nâo consigo avançar, e como dou a resposta em forma de intervalo
Chequei até este ponto:


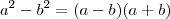 , temos que:
, temos que:
![\left(x-1 \right)\left[-2x - (x+1)\left({x}^{2} - 2 \right)\right]\leq 0 \left(x-1 \right)\left[-2x - (x+1)\left({x}^{2} - 2 \right)\right]\leq 0](/latexrender/pictures/38338842c9b7f4edd0afa4158423fbd8.png)


 . Ou seja, x = 1 é uma raiz desse polinômio. Para achar as outras, precisamos aplicar um processo de redução de grau. Tipicamente, esse processo é realizado aplicando-se o dispositivo prático de Briot-Ruffini. Após a aplicação desse processo, você deve obter:
. Ou seja, x = 1 é uma raiz desse polinômio. Para achar as outras, precisamos aplicar um processo de redução de grau. Tipicamente, esse processo é realizado aplicando-se o dispositivo prático de Briot-Ruffini. Após a aplicação desse processo, você deve obter:

Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :

