 por Cleyson007 » Sáb Mai 16, 2009 12:23
por Cleyson007 » Sáb Mai 16, 2009 12:23
Olá, bom dia!
Estou com um exercício que se pede o seguinte: Divida o polinômio

por

.
Pelo
"Método da Chave" consegui resolver sem dificuldade alguma, encontrando como resultado:
 e
e  .
.Estou encontrando muita dificuldade para efetuar a divisão usando o
"Dispositivo Prático de Briot-Ruffini". Alguém pode me ajudar explicando o procedimento passo a passo?
Desde já agradeço.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por admin » Sáb Mai 16, 2009 16:08
por admin » Sáb Mai 16, 2009 16:08
Olá
Cleyson007.
Revise suas referências bibliográficas: o dispositivo prático de Briot-Ruffini é utilizado quando o polinômio divisor é um binômio de grau 1.
O dividendo é um polinômio

, com
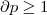
, e o divisor é um polinômio

, com

.


-

admin
- Colaborador Administrador - Professor

-
- Mensagens: 885
- Registrado em: Qui Jul 19, 2007 10:58
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática IME-USP
- Andamento: formado
 por Cleyson007 » Sáb Mai 16, 2009 23:44
por Cleyson007 » Sáb Mai 16, 2009 23:44
Olá Fabio Sousa.
Realmente

Esse detalhe acabou passando despercebido.
Muito obrigado pela dica.
Um abraço.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por Manollo » Dom Nov 22, 2009 15:05
por Manollo » Dom Nov 22, 2009 15:05
É possível dividir um polinômio p(x) por h(x) pelo dispositivo de Briot-Ruffini sim, quando p(x) é divisível por h(x). Basta fatorar o divisor. Teremos h(x) = (x - 5).(x - 1). Depois, você divide o polinômio p(x) por (x - 5) e posteriormente por (x - 1).
Cuidado com breves respostas, espere outras para ter certeza do que lhe disseram.
-
Manollo
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Dom Nov 22, 2009 14:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: matematica
- Andamento: formado
 por DeMoNaZ » Sex Abr 23, 2010 22:07
por DeMoNaZ » Sex Abr 23, 2010 22:07
Cuidado com breves respostas, espere outras para ter certeza do que lhe disseram.
Apenas Um Detalhe... P(x) Não é divisivel por H(x)
Se dividir p(x) pelas Raizes de h(x) ,Os Respectivos Restos serão Diferente de Zero..
logo pelo Teorema de D`Alembert
Se a é Uma Constante Sendo que P(x) é Divisivel por (x - a) logo P(a)= 0
e a é uma de suas raizes.

-
DeMoNaZ
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Sex Abr 23, 2010 22:02
- Formação Escolar: ENSINO MÉDIO
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de

Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é

Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:

Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:

Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:


Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 por
por  .
. e
e  .
.


 , com
, com 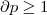 , e o divisor é um polinômio
, e o divisor é um polinômio  , com
, com  .
.


 Esse detalhe acabou passando despercebido.
Esse detalhe acabou passando despercebido.





