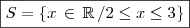por santiago alves » Sex Jul 08, 2011 08:46
Olá pessoal.
Estou com dificuldade de escrever a solução de uma inequalção do segundo grau...
ja olhei na internet, algumas outras formas de exercicios resolvidos, mais aparentemente fez foi me confundir....
o exercicio é este:
x²-5x+6<=0;
:delta encontrado=1;
raizes: x'=2;
x''=3;
Até ai, foi tranquilo, o problema é agora para escrever a solução...
pela minha analise do grafico dessas raizes, é: S={x E R / x<=2, x>=3}...
pelo o livro a resposta é: 2<=x<=3;
desde ja agradeço a ajuda, muito bom esse forum!!!!
vlws!!!!!!!!!!!
-
santiago alves
- Novo Usuário
-
- Mensagens: 7
- Registrado em: Qua Abr 20, 2011 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
por FilipeCaceres » Sex Jul 08, 2011 10:13
- parabola.png (6.2 KiB) Exibido 2605 vezes
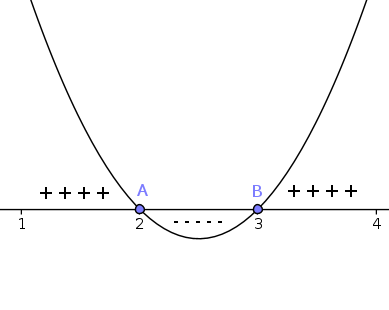
Quando tiver dúvida tente construir o gráfico, pois fazendo isso ficará fácil de ver o que se pede, observe que o que se deseja é o intervalo de A até B. Sendo assim temos que:
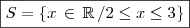
Para escrever em latex é simples, peço que leia este tutorial disponível no próprio fórum
viewtopic.php?f=9&t=74Abraço.
-
FilipeCaceres
- Colaborador Voluntário
-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
por santiago alves » Sex Jul 08, 2011 10:46
Obrigado pela orientação, foi de grande ajuda...
eu desenhei o grafico igual a vc, so q meu problema é q eu nao estava considerando que o intervalo=x,
e sim os outros numeros fora da parábola, oq me confundiu totalmente...
muito obrigado pela ajuda, espero em breve poder retribuir a alguem!!!
vlws galera!!!
-
santiago alves
- Novo Usuário
-
- Mensagens: 7
- Registrado em: Qua Abr 20, 2011 11:16
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Livro: Matematica basica para ensino Superior. pg. 59 ex4
por santiago alves » Ter Jul 12, 2011 13:45
- 2 Respostas
- 2206 Exibições
- Última mensagem por santiago alves
Ter Jul 12, 2011 14:23
Sistemas de Equações
-
- Livro: Matematica basica para ensino Superior. LOGARITMOS
por santiago alves » Sex Jul 15, 2011 00:13
- 3 Respostas
- 3227 Exibições
- Última mensagem por LuizAquino
Sex Jul 15, 2011 10:44
Logaritmos
-
- [DICA] Livro de Matemática Ensino Fundamental
por invader_zim » Seg Fev 11, 2013 14:54
- 9 Respostas
- 7769 Exibições
- Última mensagem por alex_08
Ter Fev 12, 2013 18:01
Álgebra Elementar
-
- Ensino fundamental
por dolmian » Seg Dez 10, 2012 20:32
- 1 Respostas
- 1652 Exibições
- Última mensagem por young_jedi
Seg Dez 10, 2012 22:04
Álgebra Elementar
-
- Ensino fundamental
por dolmian » Seg Dez 10, 2012 20:35
- 1 Respostas
- 1249 Exibições
- Última mensagem por e8group
Seg Dez 10, 2012 21:49
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Taxa de variação
Autor:
felipe_ad - Ter Jun 29, 2010 19:44
Como resolvo uma questao desse tipo:
Uma usina de britagem produz pó de pedra, que ao ser depositado no solo, forma uma pilha cônica onde a altura é aproximadamente igual a 4/3 do raio da base.
(a) Determinar a razão de variação do volume em relação ao raio da base.
(b) Se o raio da base varia a uma taxa de 20 cm/s, qual a razão de variação do volume quando o raio mede 2 m?
A letra (a) consegui resolver e cheguei no resultado correto de
Porem, nao consegui chegar a um resultado correto na letra (b). A resposta certa é
Alguem me ajuda? Agradeço desde já.
Assunto:
Taxa de variação
Autor:
Elcioschin - Qua Jun 30, 2010 20:47
V = (1/3)*pi*r²*h ----> h = 4r/3
V = (1/3)*pi*r²*(4r/3) ----> V = (4*pi/9)*r³
Derivando:
dV/dr = (4*pi/9)*(3r²) -----> dV/dr = 4pi*r²/3
Para dr = 20 cm/s = 0,2 m/s e R = 2 m ----> dV/0,2 = (4*pi*2²)/3 ----> dV = (3,2/3)*pi ----> dV ~= 1,066*pi m³/s
Assunto:
Taxa de variação
Autor:
Guill - Ter Fev 21, 2012 21:17
Temos que o volume é dado por:
Temos, portanto, o volume em função do raio. Podemos diferenciar implicitamente ambos os lados da equação em função do tempo, para encontrar as derivadas em função do tempo:
Sabendo que a taxa de variação do raio é 0,2 m/s e que queremos ataxa de variação do volume quando o raio for 2 m:
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
