por fernandocez » Seg Fev 14, 2011 16:42
por fernandocez » Seg Fev 14, 2011 16:42
Olá pessoal, eu sou novo aqui. Eu acho que aqui vai ser a minha única chance de aprender a resolver essa questão da prova do concurso prá magistério do Estado RJ.
A questão:
O número real x é tal que
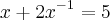
. Então, o valor de
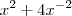
é:
No gabarito a resposta é: 21
Eu fiz arrumei ficou assim:
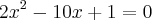
Meu delta deu 92, ai não consegui continuar. Se alguem puder ajudar agradeço.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Seg Fev 14, 2011 19:14
por LuizAquino » Seg Fev 14, 2011 19:14
fernandocez escreveu:O número real x é tal que
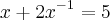
. Então, o valor de
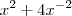
é:
Essa questão depende de você ter uma boa percepção, para notar que elevando ao quadrado ambos os membros da primeira equação a expressão
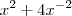
irá aparecer no primeiro membro.



Obviamente, outro caminho (mais longo) para resolver esse exercício seria desenvolver
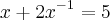
para obter a equação do 2° grau

. Em seguida, substituir as soluções dessa equação na expressão
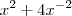
. A pessoa que escolher esse caminho verá que ele é bem mais longo do que a solução mais "elegante" apresentada acima. Além disso, é sempre bom lembrar que tempo é um fator crucial em concursos ou vestibulares.
-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
 por fernandocez » Seg Fev 14, 2011 23:16
por fernandocez » Seg Fev 14, 2011 23:16
Obrigadão Luiz, eu já vi que tenho que aprender muito prá passar no concurso e aqui é o lugar certo prá isso.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por fernandocez » Ter Fev 15, 2011 19:22
por fernandocez » Ter Fev 15, 2011 19:22
LuizAquino escreveu:
Aproveitando a sua ajuda, tem uma parecida com a resolvida que tentei, tentei de todas as formas mas não consegui chegar na resposta. Vai a questão:
26) Se

, o valor de
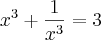
A resposta: 0
Eu fiz assim,
![{\left(x+\frac{1}{x} \right)}^{3}={\left(\sqrt[]{3} \right)}^{3} {\left(x+\frac{1}{x} \right)}^{3}={\left(\sqrt[]{3} \right)}^{3}](/latexrender/pictures/9914725c0448fa3d9b6df7e9a24a16e5.png)
, elevei ao cubo ambos os membros e comecei a desenvolver.
Só que não consegui desenvolver. Fiquei enrolado nas operações com frações, fiz assim:

= ...
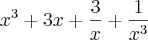
Daí eu não consegui proceguir mais. Acredito que tá errado o desenvolvimento. Obrigado pela ajuda.
-

fernandocez
- Colaborador Voluntário

-
- Mensagens: 131
- Registrado em: Seg Fev 14, 2011 15:01
- Localização: São João de Meriti - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: formado
 por LuizAquino » Ter Fev 15, 2011 20:10
por LuizAquino » Ter Fev 15, 2011 20:10
fernandocez escreveu:26) Se

, o valor de

A resposta: 0
Lembre-se que:
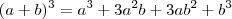
.
Além disso, lembre-se que:

.
Pois muito bem, como você havia feito, temos:

Que desenvolvendo obtemos:

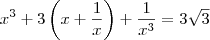


-

LuizAquino
- Colaborador Moderador - Professor

-
- Mensagens: 2654
- Registrado em: Sex Jan 21, 2011 09:11
- Localização: Teófilo Otoni - MG
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Mestrado - Modelagem Computacional
- Andamento: formado
-
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Questão prova magisterio 2008
 por fernandocez » Sáb Fev 26, 2011 11:39
por fernandocez » Sáb Fev 26, 2011 11:39
- 3 Respostas
- 2392 Exibições
- Última mensagem por LuizAquino

Sáb Fev 26, 2011 19:15
Geometria Plana
-
- PG prova concurso estado magistério 2008
por fernandocez » Sex Fev 25, 2011 20:23
- 3 Respostas
- 2323 Exibições
- Última mensagem por Molina

Sáb Fev 26, 2011 13:08
Progressões
-
- Questão prova magisterio 2007
 por fernandocez » Seg Fev 14, 2011 17:21
por fernandocez » Seg Fev 14, 2011 17:21
- 1 Respostas
- 1414 Exibições
- Última mensagem por LuizAquino

Seg Fev 14, 2011 19:57
Geometria Plana
-
- [Fração] Concurso magistério 2008
por fernandocez » Dom Jul 08, 2012 19:12
- 2 Respostas
- 2147 Exibições
- Última mensagem por fernandocez

Dom Jul 08, 2012 21:15
Álgebra Elementar
-
- Prova UNIFEI 2008
 por admin » Qua Jan 23, 2008 19:24
por admin » Qua Jan 23, 2008 19:24
- 0 Respostas
- 2840 Exibições
- Última mensagem por admin

Qua Jan 23, 2008 19:24
Vestibulares
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Funções
Autor:
Emilia - Sex Dez 03, 2010 13:24
Preciso de ajuda no seguinte problema:
O governo de um Estado Brasileiro mudou a contribuição previdenciária de seus contribuintes. era de 6% sobre qualquer salário; passou para 11% sobre o que excede R$1.200,00 nos salários. Por exemplo, sobre uma salário de R$1.700,00, a contribuição anterior era: 0,06x R$1.700,00 = R$102,00; e a atual é: 0,11x(R$1.700,00 - R$1.200,00) = R$55,00.
i. Determine as funções que fornecem o valor das contribuições em função do valor x do salário antes e depois da mudança na forma de cobrança.
ii. Esboce seus gráficos.
iii. Determine os valores de salários para os quais:
- a contribuição diminuiu;
- a contribuição permaneceu a mesma;
- a contribuição aumentou.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
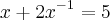 . Então, o valor de
. Então, o valor de 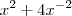 é:
é: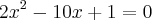

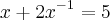 . Então, o valor de
. Então, o valor de 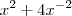 é:
é: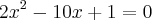

. Então, o valor de
é:
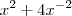 irá aparecer no primeiro membro.
irá aparecer no primeiro membro.


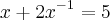 para obter a equação do 2° grau
para obter a equação do 2° grau  . Em seguida, substituir as soluções dessa equação na expressão
. Em seguida, substituir as soluções dessa equação na expressão 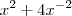 . A pessoa que escolher esse caminho verá que ele é bem mais longo do que a solução mais "elegante" apresentada acima. Além disso, é sempre bom lembrar que tempo é um fator crucial em concursos ou vestibulares.
. A pessoa que escolher esse caminho verá que ele é bem mais longo do que a solução mais "elegante" apresentada acima. Além disso, é sempre bom lembrar que tempo é um fator crucial em concursos ou vestibulares.

 , o valor de
, o valor de 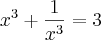
![{\left(x+\frac{1}{x} \right)}^{3}={\left(\sqrt[]{3} \right)}^{3} {\left(x+\frac{1}{x} \right)}^{3}={\left(\sqrt[]{3} \right)}^{3}](/latexrender/pictures/9914725c0448fa3d9b6df7e9a24a16e5.png) , elevei ao cubo ambos os membros e comecei a desenvolver.
, elevei ao cubo ambos os membros e comecei a desenvolver. = ...
= ... 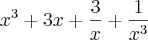

, o valor de
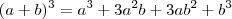 .
. .
.