Divisão de polinômios

[manuoliveira]

Dividindo-se um polinômio f por g = (x - 1)(x + 2), obtêm-se resto 2x - 1. O resto da divisão de f por x + 2 é:

Resposta: -5

[VtinxD]

Assim como números, os polinômios podem ser escritos através do algoritmo de Euclides:
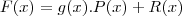.Onde F(x) é o dividendo ,g(x) o divisor , P(x) o coeficiente e R(x) o resto.
Para saber o resto da divisão de F(x) por (x+2) basta dividir os dois lados por (x+2).
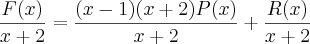.É fácil perceber que a parte (x-1)(x-2)P(x) tem resto igual a zero pois é divisivel por (x+2) então o resto da divisão de F(x) por (x+2) só pode vir do resto da divisão de R(x) por (x+2).
Utilizando o método da chave para R(x) você encontra resto igual a -5.
Espero ter ajudado.