-
-
Novo APOIA.se AjudaMatemática
por admin em Sáb Abr 25, 2020 19:01
- 0 Tópicos
- 478194 Mensagens
-
Última mensagem por admin

em Sáb Abr 25, 2020 19:01
-
-
Agradecimento aos Colaboradores
por admin em Qui Nov 15, 2018 00:25
- 0 Tópicos
- 532057 Mensagens
-
Última mensagem por admin

em Qui Nov 15, 2018 00:25
-
-
Ativação de Novos Registros
por admin em Qua Nov 14, 2018 11:58
- 0 Tópicos
- 495585 Mensagens
-
Última mensagem por admin

em Qua Nov 14, 2018 11:58
-
-
Regras do Fórum - Leia antes de postar!
por admin em Ter Mar 20, 2012 21:51
- 0 Tópicos
- 706406 Mensagens
-
Última mensagem por admin

em Ter Mar 20, 2012 21:51
-
-
DICA: Escrevendo Fórmulas com LaTeX via BBCode
por admin em Qua Ago 29, 2007 04:04
- 41 Tópicos
- 2122770 Mensagens
-
Última mensagem por Janayna

em Qui Abr 27, 2017 00:04
 por adauto martins » Qui Nov 07, 2019 14:23
por adauto martins » Qui Nov 07, 2019 14:23
vamos dar continuidade ao exerc.anterior da ENE,para estimar se o polinomio dado,tem raizes reais,o que ja mostramos ter p/ x=1,raizes complexas...
primeiramente vamos estimar o intervalo das raizes,nao o fiz na questao anterior para mostrar como é o processo de encontrar raizes racionais,que sao tambem raizes reais,pois os racionais estao contidos nos reais e etc...
vamos usar,como fiz do exerc. do ITA,usar
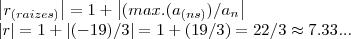
logo nosso intervalo é menor que o estimado anteriormente...ficaria agora com,para raizes racionais
[-6,-4,-3,-2,-1,-4/3,-2/3,...,2,3,4,6] o qual nao mudaria muito do anterior...vamos tomar o polinomio
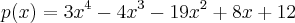
vamos usar a "regra de descartes" para variaçao de sinais dos coeficientes
(+,-,-,+,+) nao nos daria 2 trocas,ou seja duuas raizes reais positivas,ou nenhuma.como ja calculamos que para x=1,tem-se p(x)=0,logo teremos mais uma raiz positiva...
agora vamos estimar para raizes reais negativas
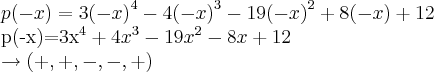
2 trocas,o qual nos da 2 raizes reais negativas ou nenhuma...
vamos agora estimar se ha raizes
complexo-conjugados
tomamos o polinomio novamente
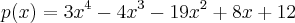
observar-se que
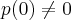
e que nao ha nenhum coeficiente nulo...
temos que

como tambem temos


como em nenhum desses encontramos a condiçao de
p/algum k,
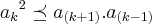
entao nao temos raiz
complexo-conjugado,pois se encontrassemos pelo um k,que satisfaz a condiçao da "regra de huat",
mesmo tendo outros que nao satisfaça tal criterio,
teriamos raizes
complexos-conjugados.
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
 por adauto martins » Sex Nov 08, 2019 12:05
por adauto martins » Sex Nov 08, 2019 12:05

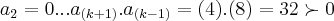
vamos pegar mais um "gancho" na questao anterior da ENE-1950 e modificarmos o polinomio para que possamos ter raizes
complexo-conjugado e encontrar a possivel localidade de suas raizes.vamos calcular o "anel",diferença entre cota-superior(disco maior) e cota inferior(disco menor).modificando o polinomio é claro que suas raizes reais serao outras,mas nosso foco serao apenas as raizes
complexo-conjugado.
(1)
cota superior(disco maior) de um polinomio p(x) é dado por:
![\left|z \right|\preceq 1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{o})/{a}_{n} \right|} \left|z \right|\preceq 1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{o})/{a}_{n} \right|}](/latexrender/pictures/77c77b019a06b99d1f1a5e75c76e67e4.png)
onde r,é a diferença entre o maior grau,e o grau subsequente do polinomio e
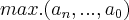
é o maior dos coeficientes de p(x),

coeficiente do monomio de maior grau...essas cotas,sao tambem cotas para o intervalo de numeros reais e mais precisas que o que estamos utilizazando,como o do exerc. do ITA,
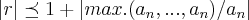
(2)
a cota inferior é dado por:
![\left|z \right|\geq 1/(1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{n})/{a}_{n} \right|}) \left|z \right|\geq 1/(1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{n})/{a}_{n} \right|})](/latexrender/pictures/0e7ec76a30c378ca9e92dd9bedc067cc.png)
onde r,é o menor dos graus do expoentes de p(x),

tomemos entao o polinomio
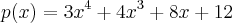
usando a "regra da lacuna" ,temos
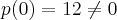
verificamos que:
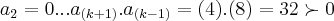
logo existe raiz
complexo-conjugado.
vamos agora estimar sua,ou suas localizaçao:
cota superior
 \right|=1+4=5
\Rightarrow \left|z \right|\preceq 5... \left|z \right|\preceq 1+\left|\sqrt[4-3]({12}/3) \right|=1+4=5
\Rightarrow \left|z \right|\preceq 5...](/latexrender/pictures/3a5bfb720b1d099f3e49845e3694f6be.png)
cota inferior
![\left|z \right|\geq 1/(1+\sqrt[2]{12/3} \right|})=1/(1+4)=1/\sqrt[]5
\left|z \right|\geq 1/\sqrt[]5 \left|z \right|\geq 1/(1+\sqrt[2]{12/3} \right|})=1/(1+4)=1/\sqrt[]5
\left|z \right|\geq 1/\sqrt[]5](/latexrender/pictures/0f29899cb03e99cdf441a028dd642a5d.png)
logo teremos

![\left|{c}_{(inf)} \right|\geq 1/\sqrt[]{5}\Rightarrow -\left|{c}_{(inf)} \right|\preceq -(1/\sqrt[]{5})
\left|{c}_{(sup)} \right|-\left|{c}_{(inf)} \right|\preceq 5-(1/\sqrt[]{5}) \left|{c}_{(inf)} \right|\geq 1/\sqrt[]{5}\Rightarrow -\left|{c}_{(inf)} \right|\preceq -(1/\sqrt[]{5})
\left|{c}_{(sup)} \right|-\left|{c}_{(inf)} \right|\preceq 5-(1/\sqrt[]{5})](/latexrender/pictures/00fb6e31e812b406213fa66b85d5635d.png)
logo as raizes
complexos-conjugado de p(x),estao localizado no disco
![\left|z \right|\preceq 5-(1/\sqrt[]{5}) \left|z \right|\preceq 5-(1/\sqrt[]{5})](/latexrender/pictures/84ab5a5e56ad55c427f7d423d0bc028c.png)
ps-como disse o estudo de soluçoes de polinomio é extensa,seja a nivel medio,como superior.e seus calculos é parte da area da matematica aplicada,calculo numerico,que faz avançar teorico,como pratico os calculos feito por computadores...
-
adauto martins
- Colaborador Voluntário

-
- Mensagens: 1171
- Registrado em: Sex Set 05, 2014 19:37
- Formação Escolar: EJA
- Área/Curso: matematica
- Andamento: cursando
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
Usuários navegando neste fórum: Nenhum usuário registrado e 10 visitantes
Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 09:10
Veja este exercício:
Se A = {

} e B = {

}, então o número de elementos A

B é:
Eu tentei resolver este exercício e achei a resposta "três", mas surgiram muitas dúvidas aqui durante a resolução.
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero?
existe inverso de zero?
zero é par, certo?
sendo x um número natural, -x é múltiplo de x?
sendo z um número inteiro negativo, z é múltiplo de z?
sendo z um número inteiro negativo, -z é múltiplo de z?
A resposta é 3?
Obrigado.
Assunto:
método de contagem
Autor:
Molina - Seg Mai 25, 2009 20:42
Boa noite, sinuca.
Se A = {

} você concorda que n só pode ser de 1 a 20? Já que pertence aos naturais?
Ou seja, quais são os divisores de 20? Eles são seis: 1, 2, 4, 5, 10 e 20.
Logo, o conjunto A é
A = {1, 2, 4, 5, 10, 20}
Se B = {

} você concorda que x será os múltiplos de 5 (positivos e negativos)? Já que m pertence ao conjunto Z?
Logo, o conjunto B é
B = {... , -25, -20, -15, -10, -5, 0, 5, 10, 15, 20, 25, ...
Feito isso precisamos ver os números que está em ambos os conjuntos, que são:
5, 10 e 20 (3 valores, como você achou).
Vou responder rapidamente suas dúvidas porque meu tempo está estourando. Qualquer dúvida, coloque aqui, ok?
sinuca147 escreveu:No processo de determinação dos elementos do conjunto B o que achei foi basicamente os múltiplos de cinco e seus opostos, daí me surgiram estas dúvidas:
existe oposto de zero? sim, é o próprio zero
existe inverso de zero? não, pois não há nenhum número que multiplicado por zero resulte em 1
zero é par, certo? sim, pois pode ser escrito da forma de 2n, onde n pertence aos inteiros
sendo x um número natural, -x é múltiplo de x? Sim, pois basta pegar x e multiplicar por -1 que encontramos -x
sendo z um número inteiro negativo, z é múltiplo de z? Sim, tais perguntando se todo número é multiplo de si mesmo
sendo z um número inteiro negativo, -z é múltiplo de z? Sim, pois basta pegar -z e multiplicar por -1 que encontramos x
A resposta é 3? Sim, pelo menos foi o que vimos a cima
Bom estudo,

Assunto:
método de contagem
Autor:
sinuca147 - Seg Mai 25, 2009 23:35
Obrigado, mas olha só este link
http://www.colegioweb.com.br/matematica ... ro-natural
neste link encontra-se a a frase:
Múltiplo de um número natural é qualquer número que possa ser obtido multiplicando o número natural por 0, 1, 2, 3, 4, 5, etc.
Para determinarmos os múltiplos de 15, por exemplo, devemos multiplicá-lo pela sucessão dos números naturais:
Ou seja, de acordo com este link -5 não poderia ser múltiplo de 5, assim como 5 não poderia ser múltiplo de -5, eu sempre achei que não interessava o sinal na questão dos múltiplos, assim como você me confirmou, mas e essa informação contrária deste site, tem alguma credibilidade?
Há e claro, a coisa mais bacana você esqueceu, quero saber se existe algum método de contagem diferente do manual neste caso:
Para determinar os elementos do conjunto A, eu tive de basicamente fazer um lista de vinte dividido por todos os números naturais maiores que zero e menores que vinte e um, finalmente identificando como elementos do conjunto A os números 1, 2, 4, 5, 10 e 20. Acho que procedi de maneira correta, mas fiquei pensando aqui se não existiria um método mais "sofisticado" e prático para que eu pudesse identificar ou ao menos contar o número de elementos do conjunto A, existe?
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
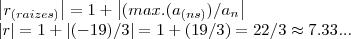
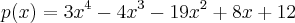
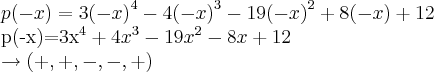
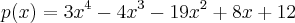
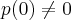 e que nao ha nenhum coeficiente nulo...
e que nao ha nenhum coeficiente nulo...


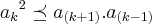



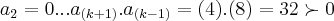 vamos pegar mais um "gancho" na questao anterior da ENE-1950 e modificarmos o polinomio para que possamos ter raizes
vamos pegar mais um "gancho" na questao anterior da ENE-1950 e modificarmos o polinomio para que possamos ter raizes ![\left|z \right|\preceq 1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{o})/{a}_{n} \right|} \left|z \right|\preceq 1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{o})/{a}_{n} \right|}](/latexrender/pictures/77c77b019a06b99d1f1a5e75c76e67e4.png)
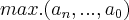

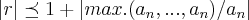
![\left|z \right|\geq 1/(1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{n})/{a}_{n} \right|}) \left|z \right|\geq 1/(1+\sqrt[r]{\left|max.({a}_{n},...,{a}_{n})/{a}_{n} \right|})](/latexrender/pictures/0e7ec76a30c378ca9e92dd9bedc067cc.png)

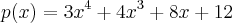
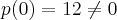
 \right|=1+4=5
\Rightarrow \left|z \right|\preceq 5... \left|z \right|\preceq 1+\left|\sqrt[4-3]({12}/3) \right|=1+4=5
\Rightarrow \left|z \right|\preceq 5...](/latexrender/pictures/3a5bfb720b1d099f3e49845e3694f6be.png)
![\left|z \right|\geq 1/(1+\sqrt[2]{12/3} \right|})=1/(1+4)=1/\sqrt[]5
\left|z \right|\geq 1/\sqrt[]5 \left|z \right|\geq 1/(1+\sqrt[2]{12/3} \right|})=1/(1+4)=1/\sqrt[]5
\left|z \right|\geq 1/\sqrt[]5](/latexrender/pictures/0f29899cb03e99cdf441a028dd642a5d.png)

![\left|{c}_{(inf)} \right|\geq 1/\sqrt[]{5}\Rightarrow -\left|{c}_{(inf)} \right|\preceq -(1/\sqrt[]{5})
\left|{c}_{(sup)} \right|-\left|{c}_{(inf)} \right|\preceq 5-(1/\sqrt[]{5}) \left|{c}_{(inf)} \right|\geq 1/\sqrt[]{5}\Rightarrow -\left|{c}_{(inf)} \right|\preceq -(1/\sqrt[]{5})
\left|{c}_{(sup)} \right|-\left|{c}_{(inf)} \right|\preceq 5-(1/\sqrt[]{5})](/latexrender/pictures/00fb6e31e812b406213fa66b85d5635d.png)
![\left|z \right|\preceq 5-(1/\sqrt[]{5}) \left|z \right|\preceq 5-(1/\sqrt[]{5})](/latexrender/pictures/84ab5a5e56ad55c427f7d423d0bc028c.png)
 } e B = {
} e B = { }, então o número de elementos A
}, então o número de elementos A  B é:
B é: