 +
+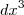 , em que a,b,c,d
, em que a,b,c,d 
 .Determine a,b,c e d para que
.Determine a,b,c e d para que 
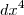

 +
+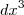 , em que a,b,c,d
, em que a,b,c,d 
 .Determine a,b,c e d para que
.Determine a,b,c e d para que 
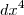

 e
e 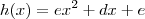 , teremos
, teremos 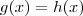 se e somente se
se e somente se 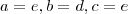 . De forma geral :
. De forma geral : 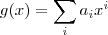 e
e 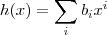 , ocorrerá
, ocorrerá  sse
sse 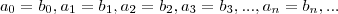 (
(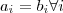 ) para todo número
) para todo número  real .
real .  e
e 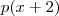 que ao substituir na equação teremos um sistema linear de 4 eq's .
que ao substituir na equação teremos um sistema linear de 4 eq's . 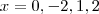 .
. temos
temos 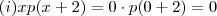 e
e 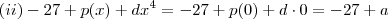
 .
.
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante

 .
.
 :
: