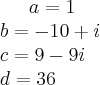Observe o seguinte,
Sejam
q: quociente
g: divisor
r: resto
f: dividendo
É verdadeira a relação,

, daí faça

onde a é uma das raízes do polinômio, nesse caso a=1+i.
g=(x-(1+i)).
Note que apesar de não conhecermos q nem r, sabemos que q é um polinômio de grau dois, visto que é o resultado da divisão de um polinômio de grau três por um polinômio de grau um, então q é do tipo
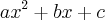
, além disso, como o grau do resto é sempre menor que o grau do divisor, então o grau de r é 0, logo r é uma constante que chamaremos de d. Por fim nossa expressão vai ficar:

Agora vc pode montar um sistema e encontrar os valores de a, b, c e d.
É um processo bastante trabalhoso, mas depois que encontrar esses valores vc vai poder escrever o polinômio

Daí poderá resolver a equação q=0 para encontrar as outras duas raízes que faltam, inclusive a raíz real. Mas novamente, dá muito trabalho.
Já adianto que,
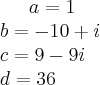
Tente chegar nesses valores para continuar a resolução.
Preste bastante atenção nesse procedimento que vc vai notar que está correto e que realmente vai chegar nos resultados, mas lhe adianto, dá muita conta.


 , daí faça
, daí faça  onde a é uma das raízes do polinômio, nesse caso a=1+i.
onde a é uma das raízes do polinômio, nesse caso a=1+i.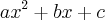 , além disso, como o grau do resto é sempre menor que o grau do divisor, então o grau de r é 0, logo r é uma constante que chamaremos de d. Por fim nossa expressão vai ficar:
, além disso, como o grau do resto é sempre menor que o grau do divisor, então o grau de r é 0, logo r é uma constante que chamaremos de d. Por fim nossa expressão vai ficar: