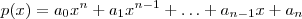 seja um polinômio de grau
seja um polinômio de grau  com coeficientes inteiros , isto é ,
com coeficientes inteiros , isto é , 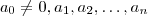 são números inteiros .Seja
são números inteiros .Seja  um número inteiro .Prove que se
um número inteiro .Prove que se  for raiz de
for raiz de  ,então
,então  será divisor do termo independente
será divisor do termo independente  .
. Solução :
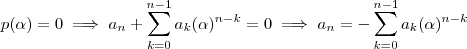
Como
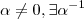 . Então ,
. Então , 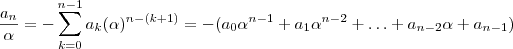 .
. Se
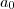 é inteiro ,
é inteiro , 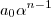 resulta um número inteiro , pois
resulta um número inteiro , pois  é inteiro
é inteiro 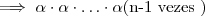 é inteiro . Assim,
é inteiro . Assim, 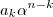 é inteiro para
é inteiro para 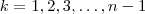 .Logo ,
.Logo , 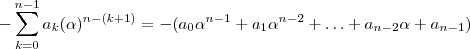 é um número inteiro e portanto
é um número inteiro e portanto  é divisível por
é divisível por  .
.A solução estar certa ? Ou não ? Se não ,como poderia provar isto ?
Agradeço desde já !


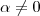 .Pois
.Pois  .
.  , acho que não se aplica
, acho que não se aplica é inteiro .Vou utilizar o seu argumento ,se
é inteiro .Vou utilizar o seu argumento ,se 

 , avisa que eu resolvo.
, avisa que eu resolvo.

