Pessoal, sou novo aqui no fórum, como não encontrei lugar pra me apresentar, estou fazendo aqui mesmo. Meu nome é Thiago Silveira e tenho 18 anos. Prazer a todos. Estou estudando pra alguns vestibulares e queria ajuda na seguinte questão de polinômios da prova da ufmg de 2007: http://www.ufmg.br/copeve/site/arquivos/Provas/2007/2etapa/2matematica.pdf
QUESTÃO 03 (Constituída de três itens.)
As dimensões a, b e c, em cm, de um paralelepípedo retângulo são as raízes do polinômio
p (x) = 6x3 – 44x2 + 103x – 77
1. CALCULE o volume desse paralelepípedo.
2. CALCULE a soma das áreas das faces desse paralelepípedo.
3. CALCULE o comprimento da diagonal desse paralelepípedo.
Eu não consegui fazer nada da questão. Nunca estudei polinômios. A unica coisa que eu pensei foi igualar p(x)=0 e tentar fazer uma equação de 3º grau, mas eu nao tenho nenhuma ideia de como que faz. Preciso de ajuda. Só me mostrarem o caminho ou me dar alguma dica de polinomios por favor
até mais e obrigado desde já.
Thiago


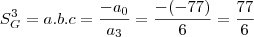
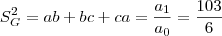
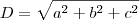
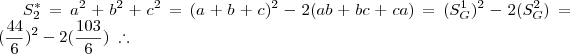
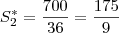
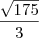 cm.
cm.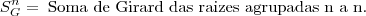 ;
;
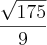 . Eu aprendi relação de Girard em função, só que foi um pouquinho diferente em que
. Eu aprendi relação de Girard em função, só que foi um pouquinho diferente em que 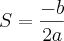 e
e 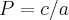 , mas eu nao sabia que podia usar assim. Eu, como eu disse nunca aprendi polinomios, fruto da "bela" educação do Brasil.
, mas eu nao sabia que podia usar assim. Eu, como eu disse nunca aprendi polinomios, fruto da "bela" educação do Brasil.