 por Cleyson007 » Seg Jan 25, 2010 20:30
por Cleyson007 » Seg Jan 25, 2010 20:30
Determine o quociente

e o resto

da divisão de

por

. Dado que
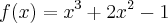
e
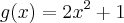
.
Efetuando a divisão de  por
por 
,
encontrei o seguinte resultado: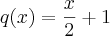
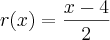
Quando fui tirar a prova real, notei que a resposta não está correta. Encontrei um resultado bem parecido:
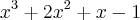
Alguém pode apresentar a resolução correta?
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por MarceloFantini » Ter Jan 26, 2010 12:08
por MarceloFantini » Ter Jan 26, 2010 12:08
Bom dia Cleyson.
Acho que você errou no sinal em algum ponto, pois o meu resto foi
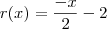
e bateu na prova real. Veja uma revisão nos cálculos!
Um abraço.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por Cleyson007 » Ter Jan 26, 2010 17:26
por Cleyson007 » Ter Jan 26, 2010 17:26
Fantini escreveu:Bom dia Cleyson.
Acho que você errou no sinal em algum ponto, pois o meu resto foi
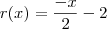
e bateu na prova real. Veja uma revisão nos cálculos!
Um abraço.
Boa tarde Fantini!
Refiz os meus cálculos e constatei que realmente errei no uso de um sinal.
O correto é:
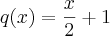
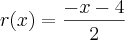
Obrigado pela ajuda!
Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7152 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
-
- Resto
por thadeu » Dom Nov 22, 2009 23:03
- 2 Respostas
- 1565 Exibições
- Última mensagem por Mathmatematica

Sáb Jun 05, 2010 05:58
Álgebra Elementar
-
- Resto Divisão
por Cleyson007 » Dom Jul 05, 2009 19:55
- 1 Respostas
- 2104 Exibições
- Última mensagem por Cleyson007

Qua Jul 08, 2009 21:08
Polinômios
-
- Resto da divisão
por ronie_mota » Dom Jul 26, 2009 16:25
- 0 Respostas
- 2538 Exibições
- Última mensagem por ronie_mota

Dom Jul 26, 2009 16:25
Álgebra Elementar
-
- Resto da divisão
por thadeu » Qua Nov 18, 2009 19:22
- 2 Respostas
- 2439 Exibições
- Última mensagem por thadeu

Dom Nov 22, 2009 17:02
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
 e o resto
e o resto  da divisão de
da divisão de  por
por  . Dado que
. Dado que 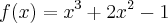 e
e 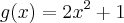 .
. por
por  , encontrei o seguinte resultado:
, encontrei o seguinte resultado: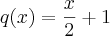
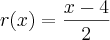
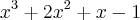



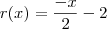 e bateu na prova real. Veja uma revisão nos cálculos!
e bateu na prova real. Veja uma revisão nos cálculos!

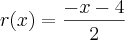


 , avisa que eu resolvo.
, avisa que eu resolvo.

