 por s1ncl41r » Seg Out 13, 2014 15:26
por s1ncl41r » Seg Out 13, 2014 15:26
Considerando a Espiral de Ulam

O polinômio
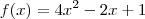
pode calcular os números da diagonal 1-3-13-31, pois:
Para
x=1 a f(1)=3
x=2 a f(2)=13
x=3 a f(3)=31
x=4 a f(4)=57
x=5 a f(5)=91
E assim por diante
É possível chegar em outros polinômios, para calcular outras diagonais e retas da Espiral de Ulam apenas chutando novos valores na expressão, como em
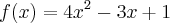
para calcular os números da reta 1-2-11-28, mas como isso é feito matematicamente falando, sem chutar valores? Por exemplo, como eu poderia criar uma expressão semelhante que me trouxesse os resultados da diagonal 1-5-17-37, e da reta 1-8-23-46, etc?
-
s1ncl41r
- Novo Usuário

-
- Mensagens: 1
- Registrado em: Seg Out 13, 2014 12:56
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia de Computação
- Andamento: cursando
 por Russman » Seg Out 13, 2014 21:00
por Russman » Seg Out 13, 2014 21:00
Um polinômio de grau n tem n parâmetros livres. Tais são as constantes reais que multiplicam as potências da variável que estão se somando. Um outras palavras, um polinômio de grau n é uma combinação linear do espaço
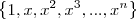
.
Assim, se eu preciso de um polinômio p(x) que calcule os números 2 e 3, por exemplo, posso dizer que p(1)=2 e p(2) = 3 e montar um sistema de equações que determine os parâmetros livres.
"Ad astra per aspera."
-
Russman
- Colaborador Voluntário

-
- Mensagens: 1183
- Registrado em: Sex Abr 20, 2012 22:06
- Formação Escolar: PÓS-GRADUAÇÃO
- Área/Curso: Física
- Andamento: formado
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Ajuda para resolver equação para calcular velocidade média
por marcorrer » Sex Fev 24, 2012 13:10
- 0 Respostas
- 3702 Exibições
- Última mensagem por marcorrer

Sex Fev 24, 2012 13:10
Sistemas de Equações
-
- Polinômio ajuda para resolver esta questão
por CADFBE » Seg Jul 06, 2015 12:53
- 1 Respostas
- 2939 Exibições
- Última mensagem por DanielFerreira

Ter Jul 07, 2015 21:30
Polinômios
-
- Problema com ''soma'' de variáveis com diferentes padrões
por guilunesp » Qui Fev 17, 2011 10:49
- 0 Respostas
- 918 Exibições
- Última mensagem por guilunesp

Qui Fev 17, 2011 10:49
Álgebra Elementar
-
- problema para calcular idade
por Angela Pimenta » Qui Out 27, 2011 14:44
- 3 Respostas
- 2933 Exibições
- Última mensagem por Angela Pimenta

Seg Out 31, 2011 18:18
Funções
-
- [Integral] para calcular volume
por neoreload » Sex Nov 21, 2014 05:26
- 1 Respostas
- 4623 Exibições
- Última mensagem por felipederaldino

Qua Nov 26, 2014 11:16
Cálculo: Limites, Derivadas e Integrais
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.

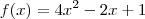 pode calcular os números da diagonal 1-3-13-31, pois:
pode calcular os números da diagonal 1-3-13-31, pois: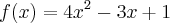 para calcular os números da reta 1-2-11-28, mas como isso é feito matematicamente falando, sem chutar valores? Por exemplo, como eu poderia criar uma expressão semelhante que me trouxesse os resultados da diagonal 1-5-17-37, e da reta 1-8-23-46, etc?
para calcular os números da reta 1-2-11-28, mas como isso é feito matematicamente falando, sem chutar valores? Por exemplo, como eu poderia criar uma expressão semelhante que me trouxesse os resultados da diagonal 1-5-17-37, e da reta 1-8-23-46, etc?

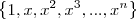 .
.
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
