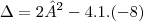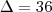por Monyk Lemos Matos » Seg Set 15, 2014 10:17
por Monyk Lemos Matos » Seg Set 15, 2014 10:17
Determine o polinômio p(x) e suas raízes, sabendo que gr(p)=2, p(3)=7, p(-1)=-9 e p(0)= -8.
-
Monyk Lemos Matos
- Novo Usuário

-
- Mensagens: 2
- Registrado em: Seg Set 15, 2014 10:00
- Formação Escolar: ENSINO MÉDIO
- Andamento: cursando
 por Diofanto » Ter Set 16, 2014 01:20
por Diofanto » Ter Set 16, 2014 01:20
Queremos encontrar um Polinômio p(x)
gr(p) = 2, logo p(x) será da forma ax²+bx+c
então p(x) = ax²+bx+c
Temos que:
p(3)=7 e p(3) = a.3²+b.3+c = 9a+3b+6
logo: 9a+3b+6 = 7
p(-1)=-9 e p(-1) = a(-1)²+b.(-1) +c = a-b+c
Logo: a-b+c = -9
p(0)= -8 e p(0) = c
logo c = -8
Teremos um sistema para determinar a, b e c, e assim, determinar p(x)
{ 9a+3b+c = 7
{ a -b+c = -9
{ c = -8
{9a+3b-8 = 7
{a - b-8 = -9
{9a+3b = 15
{a-b = -1
{3a+b = 5
{a-b = -1
Somando as duas equações teremos:
(3a + a)+(b-b)= (5-1)
4a = 4
a = 1
de (2) temos que a - b = -1
1 - b = -1
-b = -1-1
-b = -2
b=2
Logo p(x) = x²+2x-8
Achando as raízes:
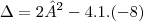
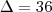

x1 =

x2 =

Espero ter ajudado
" A Matemática é o alfabeto com o qual Deus fez o Universo"
-

Diofanto
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Qui Set 20, 2012 15:39
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura e Bacharelado em Matemática
- Andamento: cursando
-
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- divisão de polinomio
por ALININA » Sáb Ago 13, 2011 07:27
- 1 Respostas
- 1320 Exibições
- Última mensagem por Caradoc

Sáb Ago 13, 2011 12:27
Polinômios
-
- divisão de polinômio
por Andreza » Qua Nov 02, 2011 11:29
- 1 Respostas
- 1233 Exibições
- Última mensagem por Paulo4114

Qui Nov 03, 2011 05:50
Polinômios
-
- Divisão de polinomio
por Ana Carla » Ter Fev 26, 2013 19:45
- 11 Respostas
- 6353 Exibições
- Última mensagem por Cleyson007

Sex Mar 01, 2013 09:06
Polinômios
-
- Divisão de polinômio
por Monyk Lemos Matos » Seg Set 15, 2014 10:13
- 0 Respostas
- 1332 Exibições
- Última mensagem por Monyk Lemos Matos

Seg Set 15, 2014 10:13
Polinômios
-
- [polinômio]Relações de Girard + raízes de polinômio
por matano2104 » Qui Set 05, 2013 17:02
- 1 Respostas
- 7155 Exibições
- Última mensagem por young_jedi

Qui Set 05, 2013 17:57
Polinômios
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
função demanda
Autor:
ssousa3 - Dom Abr 03, 2011 20:55
alguém poderia me ajudar nesse exercício aqui Uma loja de CDs adquire cada unidade por R$20,00 e a revende por R$30,00. Nestas condições,
a quantidade mensal que consegue vender é 500 unidades. O proprietário estima que, reduzindo o preço para R$28,00, conseguirá vender 600 unidades por mês.
a) Obtenha a função demanda, supondo ser linear
Eu faço ensino médio mas compro apostilas de concursos para me preparar para mercado de trabalho e estudar sozinho não é fácil. Se alguém puder me ajudar aqui fico grato
Assunto:
função demanda
Autor:
ssousa3 - Seg Abr 04, 2011 14:30
Gente alguém por favor me ensine a calcular a fórmula da função demanda

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.