Bom dia Priscilla, tudo bem?
Vou te dar as dicas, ok?
Se p(x) é divisível por x-2 e por x-1, logo x=2 e x =1 são raízes de p(x).
Para x=2, temos: p(x) = (2)^4 -3 (2)^3 + (a) (2)² +b (2) + 4 =0 --> 16 - 24 + 4a + 2b + 4 = 0 --> 4a + 2b = 4 (I)
Para x=1, temos: p(x) = (1)^4 -3 (1)^3 + (a) (1)² + (b) (1) + 4 = 0 --> 1 - 3 + a + b + 4 = 0 --> a + b = -2 (II)
Agora monte o sistema com as duas equações que encontramos (I) e (II). Você encontrará a=4 e b=-6.
Substituindo os valores de a=4 e b=-6 em p(x), temos: p(x) = x^4 -3x^3 + 4x² -6x + 4
Utilize o método das chaves para efetuar a divisão de p(x) por x+1 e encontrará 18 como resto.
Qualquer dúvida comente

Atenciosamente,
Cleyson007
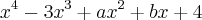 , em que a e b são números reais, é
, em que a e b são números reais, é
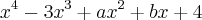 , em que a e b são números reais, é
, em que a e b são números reais, é



