 por jvabatista » Qua Abr 18, 2012 01:42
por jvabatista » Qua Abr 18, 2012 01:42
Olá.
Estou com problemas para resolver isto:
![\frac{8{x}^{\frac{3}{5}}-2\sqrt[3]{{x}^{2}}+{x}^{\frac{4}{5}}}{\sqrt[2]{{x}^{5}}} \frac{8{x}^{\frac{3}{5}}-2\sqrt[3]{{x}^{2}}+{x}^{\frac{4}{5}}}{\sqrt[2]{{x}^{5}}}](/latexrender/pictures/e143555ff719c2230efe0af738ac184b.png)
**Divida, deixando aparecer somente expoentes positivos
Separei cada membro de cima com o mesmo denominador, dividi cada um dos três separadamente e encontrei isto:
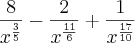
Não sei como simplificar mais do que isso e a resposta no livro é
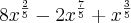
.
Tentei resolver pelo método das chaves mas obtive o mesmo resultado. Há algum outro método para se chegar ao resultado do livro ou algo mais a simplificar de até onde calculei ?
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Qua Abr 18, 2012 23:08
por DanielFerreira » Qua Abr 18, 2012 23:08
![\frac{8x^{\frac{3}{5}} - 2\sqrt[3]{x^2} + x^{\frac{4}{5}}}{\sqrt[]{x^5}} = \frac{8x^{\frac{3}{5}} - 2\sqrt[3]{x^2} + x^{\frac{4}{5}}}{\sqrt[]{x^5}} =](/latexrender/pictures/1a18ed8f0b2fb137f222168efa9eb9b5.png)
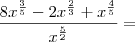
Aplicando MMC vamos deixar os denominadores iguais:
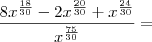
Acho que agora vc consegue, tente!
Qualquer dúvida retorne.
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jvabatista » Qui Abr 26, 2012 17:49
por jvabatista » Qui Abr 26, 2012 17:49
Oi, tentei resolver aplicando o MMC, da mesma forma que fiz o anterior - separei cada termo com seu denominador -, ficando:
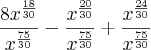
.
Mas ainda continuo obtendo o mesmo resultado de anteriormente. Há outro meio de seguir a equação que não seja este que utilizei ?
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Qui Abr 26, 2012 20:13
por DanielFerreira » Qui Abr 26, 2012 20:13
jvabatista escreveu:Oi, tentei resolver aplicando o MMC, da mesma forma que fiz o anterior - separei cada termo com seu denominador -, ficando:
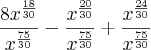
.
Mas ainda continuo obtendo o mesmo resultado de anteriormente. Há outro meio de seguir a equação que não seja este que utilizei ?
Você esqueceu de colocar o 2 (termo negativo).
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jvabatista » Qui Abr 26, 2012 20:52
por jvabatista » Qui Abr 26, 2012 20:52
Desculpe, é verdade. Esqueci o 2 quando digitei a expressão. Mas ela continua dando o mesmo resultado.
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Qui Abr 26, 2012 21:15
por DanielFerreira » Qui Abr 26, 2012 21:15
jvabatista escreveu:Desculpe, é verdade. Esqueci o 2 quando digitei a expressão. Mas ela continua dando o mesmo resultado.
Então vamos a ela.
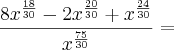
Pelo que entendi até aqui tudo bem, certo?!
Então, coloque
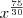
em evidência, veja:

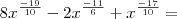
ou
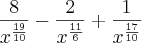
também encontrou isso?
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
 por jvabatista » Qui Abr 26, 2012 21:27
por jvabatista » Qui Abr 26, 2012 21:27
Sim. Então a resposta do livro tá errada mesmo né? rsrs. Muito obrigado.
-
jvabatista
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Seg Abr 16, 2012 22:01
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Engenharia
- Andamento: cursando
 por DanielFerreira » Dom Abr 29, 2012 00:42
por DanielFerreira » Dom Abr 29, 2012 00:42
jvabatista escreveu:Sim. Então a resposta do livro tá errada mesmo né? rsrs. Muito obrigado.
De acordo!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Polinômios
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- fatoração de polinomios
por theSinister » Ter Mai 10, 2011 20:23
- 1 Respostas
- 1764 Exibições
- Última mensagem por MarceloFantini

Ter Mai 10, 2011 21:33
Álgebra Elementar
-
- [Polinomios] Fatoração
por carvalhothg » Ter Set 20, 2011 18:08
- 3 Respostas
- 1956 Exibições
- Última mensagem por MarceloFantini

Ter Set 20, 2011 19:19
Polinômios
-
- Fatoração de polinômios
por Danilo » Sáb Jul 28, 2012 12:45
- 2 Respostas
- 1691 Exibições
- Última mensagem por Danilo

Sáb Jul 28, 2012 14:03
Polinômios
-
- Fatoração de polinômios
por Danilo » Sex Ago 16, 2013 16:51
- 3 Respostas
- 2346 Exibições
- Última mensagem por Danilo

Sex Ago 16, 2013 18:16
Polinômios
-
- Fatoração de Polinômios
por matheus_frs1 » Sex Mar 18, 2016 22:49
- 1 Respostas
- 1975 Exibições
- Última mensagem por DanielFerreira

Sáb Jul 16, 2016 23:08
Álgebra Elementar
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
(FGV) ... função novamente rs
Autor:
my2009 - Qua Dez 08, 2010 21:48
Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
Assunto:
(FGV) ... função novamente rs
Autor: Anonymous - Qui Dez 09, 2010 17:25
Uma função de 1º grau é dada por

.
Temos que para

,

e para

,

.

Ache o valor de

e

, monte a função e substitua

por

.
Assunto:
(FGV) ... função novamente rs
Autor:
Pinho - Qui Dez 16, 2010 13:57
my2009 escreveu:Uma função polinomial f do 1° grau é tal que f(3) = 6 e f(4) = 8.Portanto o valor de f(10) é :
f(x)= 2.x
f(3)=2.3=6
f(4)=2.4=8
f(10)=2.10=20
Assunto:
(FGV) ... função novamente rs
Autor:
dagoth - Sex Dez 17, 2010 11:55
isso ai foi uma questao da FGV?
haahua to precisando trocar de faculdade.
Assunto:
(FGV) ... função novamente rs
Autor:
Thiago 86 - Qua Mar 06, 2013 23:11
Saudações!

ví suaquestão e tentei resolver, depois você conta-me se eu acertei.
Uma função de 1º grau é dada por y=3a+b
Resposta :
3a+b=6 x(4)
4a+b=8 x(-3)
12a+4b=24
-12a-3b=-24
b=0
substituindo b na 1°, ttenho que: 3a+b=6
3a+0=6
a=2
substituindo em: y=3a+b
y=30+0
y=30

Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
![\frac{8{x}^{\frac{3}{5}}-2\sqrt[3]{{x}^{2}}+{x}^{\frac{4}{5}}}{\sqrt[2]{{x}^{5}}} \frac{8{x}^{\frac{3}{5}}-2\sqrt[3]{{x}^{2}}+{x}^{\frac{4}{5}}}{\sqrt[2]{{x}^{5}}}](/latexrender/pictures/e143555ff719c2230efe0af738ac184b.png)
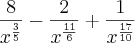
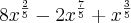 .
.

![\frac{8x^{\frac{3}{5}} - 2\sqrt[3]{x^2} + x^{\frac{4}{5}}}{\sqrt[]{x^5}} = \frac{8x^{\frac{3}{5}} - 2\sqrt[3]{x^2} + x^{\frac{4}{5}}}{\sqrt[]{x^5}} =](/latexrender/pictures/1a18ed8f0b2fb137f222168efa9eb9b5.png)
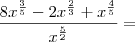
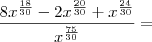

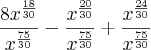 .
.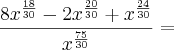
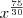 em evidência, veja:
em evidência, veja:
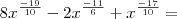
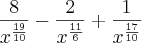
 .
. ,
,  e para
e para  ,
,  .
.
 e
e  , monte a função e substitua
, monte a função e substitua  por
por  .
.
