Obrigado pela ajuda.
No item 2b Se eu fizer 3t = 2x( x + 1) e encontrar f(3t) = (-15t+4)/(3t-2) eu estaria achando f(3x)?
Ajudem ae.
Senhor, tigre...
Na primeira questão precisamos verificar antes de tudo a inversibilidade da função y = f(x).
A inversibilidade (ou invertibilidade, sei lá eu) é um conceito que está diretamente ligado ao conceito de Bijeção.
Uma função é bijetora se e somente se: para TODO 'Y' pertencente á imagem da função existe um 'X'
UNICO pertencente ao dominio de tal forma que y = f(x)
Em linguagem matemática:
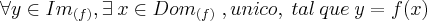
Verificando:
Suponha dois elementos diferentes no domínio que geram a mesma imagem. sejam

e



(Se voce chegar à conclusão que isso só será valido se

ela é inversível.
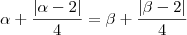

no caso ela é inversível. não esixte escolha de numeros alfa e beta diferentes que satisfazem essa igualdade.
agora para explicitar a inversa...:
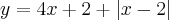
mude y por x:
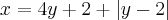
tente isolar y:

olha, sinceramente eu pensei mto e a partir dai nao saberia explicitar se nao fosse dividindo em dois casos.

ai vc faz a outra parte de y < 2 e ve lá o q vc obtém... vc vai chegar numa daquelas funções de chaves, sabe ?
pra verificar se é inversível vc tbm pode sempre plotar o gráfico da função e verificar se é bijetora ou nao.
Agora quanto à questão 2. fica dificil saber o que voce quer. Não sei qual o nivel da aula, se é matemática essencial, se é cálculo diferencial.
Mas o que voce pode tentar fazer é, considere a função g:

e a composta
 = 3x - 2 \left[f \circ g \right](x) = 3x - 2](/latexrender/pictures/dc58f6746116151f1be7a2049214d3dd.png)
(obs, eu nao tenho NENHUMA certeza disso que vou fazer agora.)
se eu achar um numero que quando eu substituo na 'g' eu obtenho ouuutro numero que quando eu substituo na composta eu obtenho 7 o problema acaba. entao:


isola x em (2):
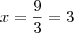
coloca isso em (1):

se eu entendi a questao a resposta do 2 a) é isso.
tente o b) no mesmo pique.[/quote]



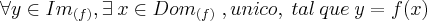
 e
e 

 (Se voce chegar à conclusão que isso só será valido se
(Se voce chegar à conclusão que isso só será valido se  ela é inversível.
ela é inversível.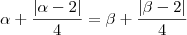

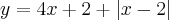
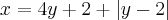



 = 3x - 2 \left[f \circ g \right](x) = 3x - 2](/latexrender/pictures/dc58f6746116151f1be7a2049214d3dd.png)


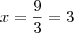


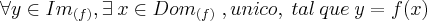
 e
e 

 (Se voce chegar à conclusão que isso só será valido se
(Se voce chegar à conclusão que isso só será valido se  ela é inversível.
ela é inversível.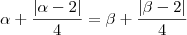

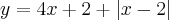
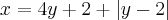



 = 3x - 2 \left[f \circ g \right](x) = 3x - 2](/latexrender/pictures/dc58f6746116151f1be7a2049214d3dd.png)


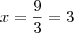


![\frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}} \frac{\sqrt[]{\sqrt[4]{8}+\sqrt[]{\sqrt[]{2}-1}}-\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}-1}}}{\sqrt[]{\sqrt[4]{8}-\sqrt[]{\sqrt[]{2}+1}}}](/latexrender/pictures/981987c7bcdf9f8f498ca4605785636a.png)
![\sqrt[]{2} \sqrt[]{2}](/latexrender/pictures/f21662d1cabab6e8b273a4b6f1cd663a.png) (dica : igualar a expressão a
(dica : igualar a expressão a  e elevar ao quadrado os dois lados)
e elevar ao quadrado os dois lados)