O livro deu um exemplo e passou algumas questões, mas uma delas foge o padrão do exemplo e eu não estou conseguindo resolver.
Equações Diferenciais, Boyce e DiPrima, Seção 4.2, Ex 8
Determine a raiz do número complexo dado]
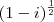
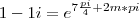

Como prosseguir? Não sei como calcular o cos e o sen de 7/8 pi...
Resposta do livro:
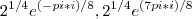


 é o seguinte:
é o seguinte: , então:
, então: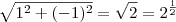 e
e .
.![(1 -i)^{\frac{1}{2}} = {(2^{\frac{1}{2}})^{\frac{1}{2}}} \left[ cos(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) + i sen(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) \right] = 2^{\frac{1}{4}} \left[ cos(- \frac{\pi}{8} ) + i sen(- \frac{\pi}{8} ) \right] (1 -i)^{\frac{1}{2}} = {(2^{\frac{1}{2}})^{\frac{1}{2}}} \left[ cos(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) + i sen(- \frac{\frac{\pi}{4}}{\frac{1}{2}}) \right] = 2^{\frac{1}{4}} \left[ cos(- \frac{\pi}{8} ) + i sen(- \frac{\pi}{8} ) \right]](/latexrender/pictures/f6c287b03bbe475a54a999b5f7efb503.png) .
.![\left[ cos(- \frac{\pi}{8}) + i sen(- \frac{\pi}{8}) \right] = e^{ - i \frac{\pi}{8}} \left[ cos(- \frac{\pi}{8}) + i sen(- \frac{\pi}{8}) \right] = e^{ - i \frac{\pi}{8}}](/latexrender/pictures/3fefbd69e0c86649186473151f871d12.png) .
. .
.