 por Angelica Abdalla » Qua Jul 06, 2011 23:12
por Angelica Abdalla » Qua Jul 06, 2011 23:12
olá estou tentando resolver esta questão "Para z=?3/2+1/2 i, calcule 1+z+z^2+z^3+?+z^50", resolvi até z^12 e sei que nesta fecha o ciclo trigonométrico, como faço para resolver???? Alguém pode me auxiliar.
-
Angelica Abdalla
- Novo Usuário

-
- Mensagens: 4
- Registrado em: Qua Jun 29, 2011 22:48
- Formação Escolar: GRADUAÇÃO
- Área/Curso: licenciatura em matemática
- Andamento: cursando
 por Molina » Qui Jul 07, 2011 00:20
por Molina » Qui Jul 07, 2011 00:20
Boa noite, Angelica.
Você percebeu então que



...
Perceba que você pode agrupar esses 13 números que você percebeu que fazem parte do ciclo, não há necessidades de calcular todos depois. Some estes do ciclo e multiplique por 4, pois assim você está somando 4*13=52 números. Agora reflita, já que você só tem 51 números para somar... Qual número foi somado uma vez a mais?

Diego Molina |
CV |
FB |
.COMEquipe AjudaMatemática.com"Existem 10 tipos de pessoas: as que conhecem o sistema binário e as que não conhecem."
-

Molina
- Colaborador Moderador - Professor

-
- Mensagens: 1551
- Registrado em: Dom Jun 01, 2008 14:10
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - UFSC
- Andamento: formado
 por MarceloFantini » Qui Jul 07, 2011 00:43
por MarceloFantini » Qui Jul 07, 2011 00:43
Outro jeito é perceba que isto é uma PG, com primeiro termo 1 e razão z. Logo, basta calcular a soma com

:
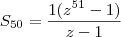
Agora é simplificar isso.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por FilipeCaceres » Qui Jul 07, 2011 10:52
por FilipeCaceres » Qui Jul 07, 2011 10:52
MarceloFantini escreveu:... calcular a soma com

:
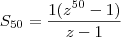
Agora é simplificar isso.
Acho que cometeu um pequeno equivoco no valor de "n", observe que temos 51 termos e não 50, sendo assim devemos usar

.
Abraço.
-
FilipeCaceres
- Colaborador Voluntário

-
- Mensagens: 351
- Registrado em: Dom Out 31, 2010 21:43
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Tec. Mecatrônica
- Andamento: formado
 por MarceloFantini » Qui Jul 07, 2011 14:14
por MarceloFantini » Qui Jul 07, 2011 14:14
Perdão pelo erro. Arrumado.
Futuro MATEMÁTICO
-
MarceloFantini
- Colaborador Moderador

-
- Mensagens: 3126
- Registrado em: Seg Dez 14, 2009 11:41
- Formação Escolar: GRADUAÇÃO
- Andamento: formado
 por vivi » Qui Jul 07, 2011 22:53
por vivi » Qui Jul 07, 2011 22:53
Por acaso essa soma fica mais ou menos assim?
4(?3/2-1/2 i)+4(1/2+?3/2)+2i
-
vivi
- Novo Usuário

-
- Mensagens: 7
- Registrado em: Dom Jun 26, 2011 19:14
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
 por vanessafey » Dom Jul 10, 2011 13:50
por vanessafey » Dom Jul 10, 2011 13:50
Também estou com dúvidas nesta questão... e fiz de maneira diferente...

Logo,
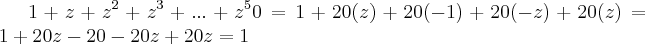
Seria isso???
-
vanessafey
- Usuário Ativo

-
- Mensagens: 20
- Registrado em: Sex Jun 24, 2011 13:24
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática
- Andamento: cursando
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17104 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- Numeros complexos!
por Estela » Seg Mar 17, 2008 00:57
- 7 Respostas
- 13316 Exibições
- Última mensagem por andegledson

Seg Nov 02, 2009 21:41
Números Complexos
-
- Números Complexos
por michelle » Dom Ago 31, 2008 15:35
- 3 Respostas
- 10316 Exibições
- Última mensagem por admin

Dom Ago 31, 2008 21:00
Números Complexos
-
- Números Complexos
por Cleyson007 » Qui Mai 14, 2009 13:57
- 7 Respostas
- 13931 Exibições
- Última mensagem por Cleyson007

Sáb Mai 16, 2009 11:04
Números Complexos
-
- NUMEROS COMPLEXOS
por lieberth » Sáb Jun 13, 2009 13:48
- 1 Respostas
- 4098 Exibições
- Última mensagem por Marcampucio

Sáb Jun 13, 2009 14:35
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.








 :
:


:
 .
.



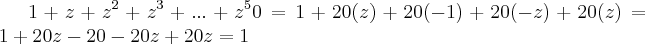



 , avisa que eu resolvo.
, avisa que eu resolvo.

