 por futuromilitar » Sáb Mai 21, 2016 14:20
por futuromilitar » Sáb Mai 21, 2016 14:20
Considere a equação
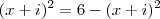
, onde x é um complexo,
![i=\sqrt[2]{i} i=\sqrt[2]{i}](/latexrender/pictures/ef3c93447f059ad717523ec424627f41.png)
e Re x>0 . O menor número natural n tal que
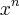
seja um imaginário puro é:
a)1
b)2
c)3
d)4
"Nenhum soldado pode combater a não ser que esteja bem abastecido de carne e cerveja''
-

futuromilitar
- Usuário Ativo

-
- Mensagens: 13
- Registrado em: Qui Mai 19, 2016 17:50
- Localização: Itapajé,Ceará,Brasil
- Formação Escolar: ENSINO MÉDIO PROFISSIONALIZANTE
- Área/Curso: Curso Técnico em Contabilidade
- Andamento: formado
 por DanielFerreira » Sáb Mai 21, 2016 16:30
por DanielFerreira » Sáb Mai 21, 2016 16:30
futuromilitar escreveu:Considere a equação
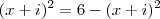
, onde x é um complexo,
![i=\sqrt[2]{i} i=\sqrt[2]{i}](/latexrender/pictures/ef3c93447f059ad717523ec424627f41.png)
e Re x>0 . O menor número natural n tal que
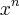
seja um imaginário puro é:
a)1
b)2
c)3d)4
Já faz algum tempo que não vejo o assunto (números complexos). Mas, vou tentar! Rs
Resolvendo a equação, temos:
![\\ (x + i)^2 = 6 - (x + i)^2 \\\\ 2 \cdot (x + i)^2 = 6 \\\\ (x + i)^2 = 3 \\\\ (x + i) = \sqrt[2]{3} \\\\ x + i = + \sqrt{3}, \ \ \text{pois} \ \ x > 0 \\\\ \boxed{x = \sqrt{3} - i} \\ (x + i)^2 = 6 - (x + i)^2 \\\\ 2 \cdot (x + i)^2 = 6 \\\\ (x + i)^2 = 3 \\\\ (x + i) = \sqrt[2]{3} \\\\ x + i = + \sqrt{3}, \ \ \text{pois} \ \ x > 0 \\\\ \boxed{x = \sqrt{3} - i}](/latexrender/pictures/6000fae3e7e7e60fc979bac2b11395f7.png)
Note que:
- quando n = 1:

Não é imaginário puro.
- quando n = 2:
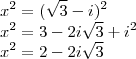
Não é imaginário puro.
- quando n = 3:
Só concluir!
"Sabedoria é saber o que fazer;
habilidade é saber como fazer;
virtude é fazer."
(David S. Jordan)
--------------------------------------------------------------------------------
-
DanielFerreira
- Colaborador - em formação

-
- Mensagens: 1732
- Registrado em: Qui Jul 23, 2009 21:34
- Localização: Mangaratiba - RJ
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Licenciatura em Matemática - IFRJ
- Andamento: formado
-
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- Equação Números Complexos
por franufscar » Sáb Mai 25, 2013 02:15
- 1 Respostas
- 6499 Exibições
- Última mensagem por futuromilitar

Sáb Mai 21, 2016 14:25
Números Complexos
-
- [Números complexos] Equação
por fff » Qua Mai 14, 2014 16:50
- 1 Respostas
- 2794 Exibições
- Última mensagem por Cleyson007

Qua Mai 14, 2014 19:15
Números Complexos
-
- [raízes de números complexos] Raízes de uma equação com grau
por karenfreitas » Seg Ago 22, 2016 19:08
- 1 Respostas
- 8109 Exibições
- Última mensagem por adauto martins

Sáb Ago 27, 2016 16:11
Números Complexos
-
- Números complexos módulo de dois números complexos important
por elisamaria » Qui Jun 11, 2015 16:56
- 1 Respostas
- 17101 Exibições
- Última mensagem por nakagumahissao

Qui Jun 11, 2015 19:20
Números Complexos
-
- complexos
por irineu junior » Dom Mar 14, 2010 15:41
- 1 Respostas
- 1938 Exibições
- Última mensagem por DanielFerreira

Seg Mar 15, 2010 04:31
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 1 visitante
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 10:38
Olá ! Tenho essa dúvida e não consigo montar o problema para resolução:
Qual é o racional não nulo cujo o quadrado é igual à sua terça parte ?
Grata.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 12:27

Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 12:55
também pensei que fosse assim, mas a resposta é

.
Obrigada Fantini.
Assunto:
Conjunto dos números racionais.
Autor:
MarceloFantini - Sex Fev 18, 2011 13:01

Como

:

O que você fez?
Assunto:
Conjunto dos números racionais.
Autor:
scggomes - Sex Fev 18, 2011 16:17
eu só consegui fazer a igualdade, não consegui desenvolver o restante, não pensei em fatoração, mas agora entendi o que vc fez.
Obrigada.
Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.
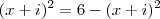 , onde x é um complexo,
, onde x é um complexo, ![i=\sqrt[2]{i} i=\sqrt[2]{i}](/latexrender/pictures/ef3c93447f059ad717523ec424627f41.png) e Re x>0 . O menor número natural n tal que
e Re x>0 . O menor número natural n tal que 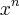 seja um imaginário puro é:
seja um imaginário puro é: 
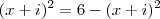 , onde x é um complexo,
, onde x é um complexo, ![i=\sqrt[2]{i} i=\sqrt[2]{i}](/latexrender/pictures/ef3c93447f059ad717523ec424627f41.png) e Re x>0 . O menor número natural n tal que
e Re x>0 . O menor número natural n tal que 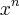 seja um imaginário puro é:
seja um imaginário puro é: 
, onde x é um complexo,
e Re x>0 . O menor número natural n tal que
seja um imaginário puro é:
![\\ (x + i)^2 = 6 - (x + i)^2 \\\\ 2 \cdot (x + i)^2 = 6 \\\\ (x + i)^2 = 3 \\\\ (x + i) = \sqrt[2]{3} \\\\ x + i = + \sqrt{3}, \ \ \text{pois} \ \ x > 0 \\\\ \boxed{x = \sqrt{3} - i} \\ (x + i)^2 = 6 - (x + i)^2 \\\\ 2 \cdot (x + i)^2 = 6 \\\\ (x + i)^2 = 3 \\\\ (x + i) = \sqrt[2]{3} \\\\ x + i = + \sqrt{3}, \ \ \text{pois} \ \ x > 0 \\\\ \boxed{x = \sqrt{3} - i}](/latexrender/pictures/6000fae3e7e7e60fc979bac2b11395f7.png)

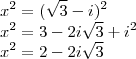


 .
.
 :
: