 por pavaroti » Dom Nov 01, 2009 23:27
por pavaroti » Dom Nov 01, 2009 23:27
Boa noite, tou com uma duvida dum exercicio que nao consigo resolve que e' o seguinte:
Determine o complexo Z = x + yi tal que:

-
pavaroti
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Nov 01, 2009 23:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: inf
- Andamento: cursando
 por Cleyson007 » Seg Nov 02, 2009 10:28
por Cleyson007 » Seg Nov 02, 2009 10:28
Bom dia Pavaroti!
Primeiramente, seja bem vindo ao Ajuda Matemática!
Pavaroti, o exercício consiste em substituir o valor de
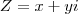
na expressão:

Lembrando que:

--> Significa o conjugado de

(O conjugado de um número complexo faz "inverter" o sinal da parte imaginária desse número --> Logo, o conjugado de

é:
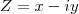
)
Jogando na expressão, temos:
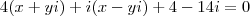
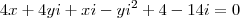
Lembrando que

------>
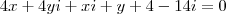 Esse é o resultado da expressão:
Esse é o resultado da expressão: 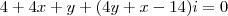
Comente qualquer dúvida

Até mais.
Bons estudos.
Editado pela última vez por
Cleyson007 em Seg Nov 02, 2009 10:40, em um total de 1 vez.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por pavaroti » Seg Nov 02, 2009 10:40
por pavaroti » Seg Nov 02, 2009 10:40
Pois eu também fiz assim no inicio mas o problema e' que não sei fazer como esta' na solução do exercício que e':
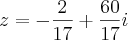
-
pavaroti
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Nov 01, 2009 23:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: inf
- Andamento: cursando
 por Cleyson007 » Seg Nov 02, 2009 11:22
por Cleyson007 » Seg Nov 02, 2009 11:22
Bom dia!
Continuando a resolução do problema:
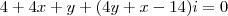

Igualando parte real com parte real e parte imaginaria com parte imaginaria teremos:
Montando o sistema:
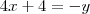

Resolvendo o sistema você encontrará:


Portanto, o número complexo é:
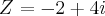
Favor, conferir o gabarito

-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
 por pavaroti » Seg Nov 02, 2009 11:50
por pavaroti » Seg Nov 02, 2009 11:50
Então a solução está mal?

-
pavaroti
- Usuário Ativo

-
- Mensagens: 10
- Registrado em: Dom Nov 01, 2009 23:04
- Formação Escolar: GRADUAÇÃO
- Área/Curso: inf
- Andamento: cursando
 por Cleyson007 » Seg Nov 02, 2009 12:41
por Cleyson007 » Seg Nov 02, 2009 12:41
pavaroti escreveu:Então a solução está mal?

Pavaroti, não encontro erro em minha solução. Vamos aguardar o que os outros membros do fórum tem a dizer

Até mais.
-

Cleyson007
- Colaborador Voluntário

-
- Mensagens: 1228
- Registrado em: Qua Abr 30, 2008 00:08
- Formação Escolar: GRADUAÇÃO
- Área/Curso: Matemática UFJF
- Andamento: formado
Voltar para Números Complexos
Se chegou até aqui, provavelmente tenha interesse pelos tópicos relacionados abaixo.
Aproveite a leitura. Bons estudos!
-
- (UFRGS) Complexo
por flavio2010 » Sáb Jul 17, 2010 12:51
- 1 Respostas
- 2065 Exibições
- Última mensagem por Tom

Sáb Jul 17, 2010 14:10
Números Complexos
-
- [módulo do número complexo]
por JKS » Qui Jun 20, 2013 01:56
- 1 Respostas
- 3055 Exibições
- Última mensagem por MateusL

Qui Jul 18, 2013 19:49
Números Complexos
-
- Equação de número complexo
 por YuriFreire » Seg Set 01, 2014 21:44
por YuriFreire » Seg Set 01, 2014 21:44
- 3 Respostas
- 5138 Exibições
- Última mensagem por adauto martins

Seg Set 22, 2014 21:19
Números Complexos
-
- somatória com número complexo
por ezidia51 » Qua Abr 04, 2018 17:44
- 3 Respostas
- 10528 Exibições
- Última mensagem por Gebe

Qui Abr 05, 2018 13:32
Números Complexos
-
- [Número Complexo] Exercício básico...
por Vennom » Sáb Jul 21, 2012 06:57
- 8 Respostas
- 19145 Exibições
- Última mensagem por Russman

Seg Set 10, 2012 15:56
Números Complexos
Usuários navegando neste fórum: Nenhum usuário registrado e 2 visitantes
Assunto:
cálculo de limites
Autor:
Hansegon - Seg Ago 25, 2008 11:29
Bom dia.
Preciso de ajuda na solução deste problema, pois só chego ao resultado de 0 sobre 0.
Obrigado
\lim_{x\rightarrow-1} x³ +1/x²-1[/tex]
Assunto:
cálculo de limites
Autor:
Molina - Seg Ago 25, 2008 13:25

Realmente se você jogar o -1 na equação dá 0 sobre 0.
Indeterminações deste tipo você pode resolver por L'Hôpital
que utiliza derivada.
Outro modo é transformar o numerador e/ou denominador
para que não continue dando indeterminado.
Dica: dividir o numerador e o denominador por algum valor é uma forma que normalmente dá certo.

Caso ainda não tenha dado uma

, avisa que eu resolvo.
Bom estudo!
Assunto:
cálculo de limites
Autor:
Guill - Dom Abr 08, 2012 16:03



Powered by phpBB © phpBB Group.
phpBB Mobile / SEO by Artodia.




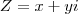 na expressão:
na expressão:
 --> Significa o conjugado de
--> Significa o conjugado de  (O conjugado de um número complexo faz "inverter" o sinal da parte imaginária desse número --> Logo, o conjugado de
(O conjugado de um número complexo faz "inverter" o sinal da parte imaginária desse número --> Logo, o conjugado de  é:
é: 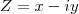 )
) 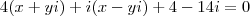
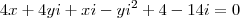
 ------>
------> 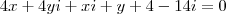


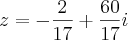

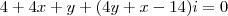

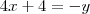



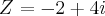








 , avisa que eu resolvo.
, avisa que eu resolvo.

